Выписали все делители натурального числа n, кроме самого числа n. оказалось, что самый большое из выписанных чисел равно 1001. сколько таких чисел n, для которые могло такое произойти?
Пусть прыжки по часовой стрелке обозначаются со знаком "плюс", а против часовой стрелке - со знаком "минус".
Найдем, какие более простые прыжки с точки зрения перемещения (то есть по модулю) можно совершить.
Изначально имеется два прыжка (+21) и (-15) Выполним их по очереди:
Итак, каким-то образом можно выполнить прыжок (+6).
Сгруппируем прыжки (+6) и (-15):
Таким образом, можно выполнить прыжок (-9).
Наконец, сгруппируем прыжки (+6) и (-9):
Также выполним прыжок (-3).
Получить прыжок с меньшим перемещением (кроме тривиально нулевого) невозможно.
Обратим внимание на то, что общее число каменей 2019, а также все рассмотренные прыжки кратны 3. Это означает, что при любом прыжке номер исходного и номер конечного камня дают одинаковые остатки при делении на 3.
Посетить все камни с номерами, дающими при делении на 3 один и тот же остаток, можно. У нас есть прыжок (-3).
Таким образом, мы посещаем либо все камни с номерами, кратными 3, либо все с номерами, дающими при делении на 3 остаток 1, либо все с номерами, дающими при делении на 3 остаток 2. И тех и других и третьих поровну в количестве штуки.
Пусть число а,b(c) периодичное, где а - целая часть, b - число в предпериоде, c - число в периоде, в нашем примере а=2, b=1, c=6. Чтобы преобразовать эту дробь в обыкновенную нужно придерживаться следующему правилу:
а) Считаем количество цифр в периоде десятичной дроби и обозначаем количество цифр через k, в нашем примере k=1, так как число 6 состоит из одной цифры;
б) Считаем количество цифр, стоящих в предпериоде, то есть количество цифр, стоящих после запятой, но до периода десятичной дроби и обозначаем количество цифр через m, в нашем примере m=1, так как число 1 состоит из одной цифры;
в) Записываем все цифры после запятой (включая цифры из периода) в виде натурального числа , в нашем примере n=16;
г) Теперь записываем все цифры, стоящие после запятой, но до периода, в виде натурального числа , в нашем примере s=1;
д) Подставляем найденные значения в формулу
Нетрудно видеть, что состоит из k цифр 9, а из m цифр 0 после 1.
В нашем примере
2) 5,14(33) ⇒ a=5, k=2, m=2, n=1433, s=14. Тогда
3) 0,11(35) ⇒ a=0, k=2, m=2, n=1135, s=11. Тогда
4) 0,214(45) ⇒ a=0, k=2, m=3, n=21445, s=214. Тогда
Пусть прыжки по часовой стрелке обозначаются со знаком "плюс", а против часовой стрелке - со знаком "минус".
Найдем, какие более простые прыжки с точки зрения перемещения (то есть по модулю) можно совершить.
Изначально имеется два прыжка (+21) и (-15) Выполним их по очереди:
Итак, каким-то образом можно выполнить прыжок (+6).
Сгруппируем прыжки (+6) и (-15):
Таким образом, можно выполнить прыжок (-9).
Наконец, сгруппируем прыжки (+6) и (-9):
Также выполним прыжок (-3).
Получить прыжок с меньшим перемещением (кроме тривиально нулевого) невозможно.
Обратим внимание на то, что общее число каменей 2019, а также все рассмотренные прыжки кратны 3. Это означает, что при любом прыжке номер исходного и номер конечного камня дают одинаковые остатки при делении на 3.
Посетить все камни с номерами, дающими при делении на 3 один и тот же остаток, можно. У нас есть прыжок (-3).
Таким образом, мы посещаем либо все камни с номерами, кратными 3, либо все с номерами, дающими при делении на 3 остаток 1, либо все с номерами, дающими при делении на 3 остаток 2. И тех и других и третьих поровну в количестве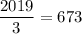
штуки.
ответ: 673
Пошаговое объяснение:
Общую схему рассмотрим в примере 1) 2,1(6).
Пусть число а,b(c) периодичное, где а - целая часть, b - число в предпериоде, c - число в периоде, в нашем примере а=2, b=1, c=6. Чтобы преобразовать эту дробь в обыкновенную нужно придерживаться следующему правилу:
а) Считаем количество цифр в периоде десятичной дроби и обозначаем количество цифр через k, в нашем примере k=1, так как число 6 состоит из одной цифры;
б) Считаем количество цифр, стоящих в предпериоде, то есть количество цифр, стоящих после запятой, но до периода десятичной дроби и обозначаем количество цифр через m, в нашем примере m=1, так как число 1 состоит из одной цифры;
в) Записываем все цифры после запятой (включая цифры из периода) в виде натурального числа , в нашем примере n=16;
г) Теперь записываем все цифры, стоящие после запятой, но до периода, в виде натурального числа , в нашем примере s=1;
д) Подставляем найденные значения в формулу
Нетрудно видеть, что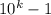
состоит из k цифр 9, а 
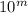из m цифр 0 после 1.
В нашем примере
2) 5,14(33) ⇒ a=5, k=2, m=2, n=1433, s=14. Тогда
3) 0,11(35) ⇒ a=0, k=2, m=2, n=1135, s=11. Тогда
4) 0,214(45) ⇒ a=0, k=2, m=3, n=21445, s=214. Тогда