1. У слові "ліцей" є 5 букв, які можна переставляти в будь-якому порядку
Відповідь: 120 слів.
2. Перше місце дістанеться одному з 10 спортсменів, друге місце — одному з 9 спортсменів, бо один уже має своє призове місце, і т. д.
Тобто маємо розміщення з 3 елементів по 10:
в
Відповідь в.
3. Вибір 2-х червоних яблук з 20: в.
Вибір 4-х жовтих яблук з 10: в.
Вибір 1-го зеленого яблука з 5: в.
Вибір 2 + 4 + 1 = 7 яблук з 20 + 10 + 5 = 35:
Нехай — подія, яка полягає в тому, що серед вибраних яблук з ящику є 2 червоних, 4 жовтих і 1 зелене.
Відповідь: 0,03.
1)Решить неравенство ((х-5)^2 (х-3)(х+2)) / ((х-4)(х+4) )≤0;
4)Решить уравнение 5²ˣ⁻¹ +2²ˣ-5²ˣ +2²ˣ⁺²=0,
5) Решить уравнение 5сtgx–8сtgx+3 = 0
Пошаговое объяснение:
1)((х-5)^2 (х-3)(х+2))/ ((х-4)(х+4) )≤0
Найдем нули : х=5,х=3,х=2,х=4,х=-4.
Метод интервалов :
(-4)[-2][3](4)[5]
( при переходе через х=5 знак (х-5)^2 остается прежним,т.к (х-5)^2≥0).
Получаем х∈(-4;2] ∪[3;4), х=5.
4)5²ˣ⁻¹ +2²ˣ-5²ˣ +2²ˣ⁺²=0,
5²ˣ⁻¹ -5²ˣ =-2²ˣ-2²ˣ⁺²,
5²ˣ (5⁻¹ -1)=2²ˣ (-1 -2²),
5²ˣ (-4/5)=2²ˣ (-5) | :(-4/5)*(2²ˣ),
5²ˣ:2²ˣ=25/4,
(5/2)²ˣ=(5/2)²,
х=1.
5) 5сtgx–8сtgx+3 = 0 , одз х≠πn n∈Z
Пусть сtg x =а;
5а²–8а+3=0
D=64-60=4, а₁=(8–2)/10=0,6 , а₂=1,2;
сtg x = 0,6 = > x=аrcсtg0,6 +π n, n∈Z ,
сtg x = 1,2 = > x=arcсtg1,2+π k, k∈Z.
1. У слові "ліцей" є 5 букв, які можна переставляти в будь-якому порядку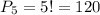
Відповідь: 120 слів.
2. Перше місце дістанеться одному з 10 спортсменів, друге місце — одному з 9 спортсменів, бо один уже має своє призове місце, і т. д.
Тобто маємо розміщення з 3 елементів по 10:
Відповідь в.
3. Вибір 2-х червоних яблук з 20: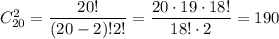
в.
Вибір 4-х жовтих яблук з 10: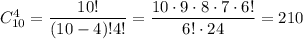
в.
Вибір 1-го зеленого яблука з 5: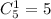
в.
Вибір 2 + 4 + 1 = 7 яблук з 20 + 10 + 5 = 35: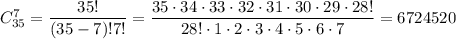
Нехай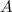
— подія, яка полягає в тому, що серед вибраних яблук з ящику є 2 червоних, 4 жовтих і 1 зелене.
Відповідь: 0,03.
1)Решить неравенство ((х-5)^2 (х-3)(х+2)) / ((х-4)(х+4) )≤0;
4)Решить уравнение 5²ˣ⁻¹ +2²ˣ-5²ˣ +2²ˣ⁺²=0,
5) Решить уравнение 5сtgx–8сtgx+3 = 0
Пошаговое объяснение:
1)((х-5)^2 (х-3)(х+2))/ ((х-4)(х+4) )≤0
Найдем нули : х=5,х=3,х=2,х=4,х=-4.
Метод интервалов :
(-4)[-2][3](4)[5]
( при переходе через х=5 знак (х-5)^2 остается прежним,т.к (х-5)^2≥0).
Получаем х∈(-4;2] ∪[3;4), х=5.
4)5²ˣ⁻¹ +2²ˣ-5²ˣ +2²ˣ⁺²=0,
5²ˣ⁻¹ -5²ˣ =-2²ˣ-2²ˣ⁺²,
5²ˣ (5⁻¹ -1)=2²ˣ (-1 -2²),
5²ˣ (-4/5)=2²ˣ (-5) | :(-4/5)*(2²ˣ),
5²ˣ:2²ˣ=25/4,
(5/2)²ˣ=(5/2)²,
х=1.
5) 5сtgx–8сtgx+3 = 0 , одз х≠πn n∈Z
Пусть сtg x =а;
5а²–8а+3=0
D=64-60=4, а₁=(8–2)/10=0,6 , а₂=1,2;
сtg x = 0,6 = > x=аrcсtg0,6 +π n, n∈Z ,
сtg x = 1,2 = > x=arcсtg1,2+π k, k∈Z.