X:6=54
за домашку оценку ставят! ​

(1 вариант решения)Т.к в магазин завезли 63 кг овощей , а 7/9 из общего количества составляла морковь , то найдём 1/9 из всех овощей , то есть 63:9=7 кг ( это 1/9 от ВСЕХ овощей) , по условию морковь 7/9 , следовательно умножим 7*7=49кг моркови завезли в магазин

(2 вариант решения ( тоже самое , что и первый только не расписан)

из известного 7/9 морковь , 63 кг (все овощи) , следовательно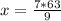 (х-неизвестное кол-во моркови(кг)), сокращаем в дроби 63 и 9 ( по таблице умножения 9 * 7 = 63 ) то есть 63:9 =7 ,следовательно x=7*7=49кг моркови.

* * * * * * * * * * * * * * * * * * * * * * * * * *

Найти экстремумы функции 9.  z = 5x² + 2xy -y² - 10x -2y -5

ответ:   экстремума нет

Пошаговое объяснение:

Алгоритм исследования функции z=f(x,y) на экстремум

Найти  частные производные ∂z/∂x и ∂z/∂y. Составить и решить систему уравнений { ∂z/∂x=0 ; ∂z/∂y=0. ( Точки, координаты которых удовлетворяют указанной системе, называют стационарными. )

∂z/∂x=10x +2y - 10 =2(5x+y -5)  ; ∂z/∂y=2x-2y -2=2(x-y -1)

{2(5x+y -5) =0 ; 2(x-y -1) =0 ⇔ { 5x+y = 5 ; x - y = 1 .⇔ { x = 1 ;  y = 0 .

M₀ (1 ; 0 ) _единственная  стационарная  точка.

Найдем   ∂²z/∂x², ∂²z/∂x∂y, ∂²z/∂y²  в стационарной точке

( в  данной  задаче  все они  постоянные ) :

∂²z/∂x²=(10x +2y -10) 'ₓ = 10 ; ∂²z/∂x∂y=(10x +2y -10) ' у =2 ;

∂²z/∂y² =(2x-2y -2)' у =  - 2 .

Вычисляем  значение  Δ =  AC - B²  

* * * A = ∂²z/∂x² ; B = ∂²z/∂x∂y ;  C =∂²z/∂y²  * * *

Δ = 10*(-2) -2² = - 24 < 0     ⇒  экстремума нет .