В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа будет являться число .
В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси ).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
Число в математике, по определению, равно отношению длинны произвольной окружности к диаметру той же окружности, поскольку все окружности подобны друг другу, т.е.:
;
Отсюда: формула [1] ;
Если же нам нужно найти длину не всей окружности, а только длину дуги составляющую часть от длины всей окружности, в данном конкретном случае от длины всей окружности, то нам просто нужно умножить длину всей окружности на эту самую часть
Таким образом, получаем, что:
формула [2] ;
Теперь воспользуемся формулами [1] и [2] и рассчитаем конкретные значения для данной задачи, учитывая, что:
Пошаговое объяснение:
Точка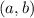 на комплексной плоскости изображает число
на комплексной плоскости изображает число 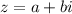
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа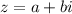 будет являться число
будет являться число 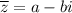 .
.
В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси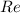 ).
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
Отсюда:
Если же нам нужно найти длину не всей окружности, а только длину дуги
Таким образом, получаем, что:
Теперь воспользуемся формулами [1] и [2] и рассчитаем конкретные значения для данной задачи, учитывая, что:
О т в е т :