Число 2011 оканчивается на 1, поэтому при возведении 2011 в любую степень результат будет оканчиваться на 1, в том числе и 2011^2013.
Число 2012 оканчивается на 2, квадрат этого числа будет оканчиваться на 4, куб - на 8, четвёртая степень - на 6, пятая степень - снова на 2, шестая - на 4, седьмая - на 8, восьмая - на 6 и т. д., т.е. через 4 числа цифра повторяется. Так как 2014=503*4+2, то число 2012^2014 оканчивается такой же цифрой, что и 2012^2, то есть 4.
Первый результат оканчивается на 1, второй - на 4.
1+4=5
Значит, полученная сумма будет делиться на 5, следовательно, не будет являться простым числом.
нет, не является. Докажем, что получившееся число чётное.
Перепишем исходное выражение в виде
2011^2013 + ((2011+1)^2013)*2012 и разложим скобку по биному Ньютона.
(2011+1)^2013 = Ckn*2011^(n*k)*1^k
вынесем из этой суммы первый и последний члены; оставшиеся члены в сумме составляют 2012 слагаемых, в каждое из которых входит 2011 в какой-то степени.Обозначу устаток за А.
Итак, исходное выражение в итоге равно:
2011^2013+2012*(2011^2013+A+1)=
2011^2013(1+2012) + 2012*A+ 2012
2011^2013 * (1+2012) чётное
А представляет собой сумму вида С1*2011^2010+ C2*2011^2009+ ... + C2012*2011
т.е. чётных и нечётных слагаемых поровну, следовательно, А чётное.
Нет, не является.
Число 2011 оканчивается на 1, поэтому при возведении 2011 в любую степень результат будет оканчиваться на 1, в том числе и 2011^2013.
Число 2012 оканчивается на 2, квадрат этого числа будет оканчиваться на 4, куб - на 8, четвёртая степень - на 6, пятая степень - снова на 2, шестая - на 4, седьмая - на 8, восьмая - на 6 и т. д., т.е. через 4 числа цифра повторяется. Так как 2014=503*4+2, то число 2012^2014 оканчивается такой же цифрой, что и 2012^2, то есть 4.
Первый результат оканчивается на 1, второй - на 4.
1+4=5
Значит, полученная сумма будет делиться на 5, следовательно, не будет являться простым числом.
нет, не является. Докажем, что получившееся число чётное.
Перепишем исходное выражение в виде
2011^2013 + ((2011+1)^2013)*2012 и разложим скобку по биному Ньютона.
(2011+1)^2013 =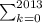 Ckn*2011^(n*k)*1^k
Ckn*2011^(n*k)*1^k
вынесем из этой суммы первый и последний члены; оставшиеся члены в сумме составляют 2012 слагаемых, в каждое из которых входит 2011 в какой-то степени.Обозначу устаток за А.
Итак, исходное выражение в итоге равно:
2011^2013+2012*(2011^2013+A+1)=
2011^2013(1+2012) + 2012*A+ 2012
2011^2013 * (1+2012) чётное
А представляет собой сумму вида С1*2011^2010+ C2*2011^2009+ ... + C2012*2011
т.е. чётных и нечётных слагаемых поровну, следовательно, А чётное.
2012*А чётное
2012 чётное, их сумма тоже чётное число.
ЧТД