Из посёлка A выехал легковой автомобиль со скоростью 80 км/ч, а из посёлка Б выехал грузовик со скоростью 60 км/ч. Через 2 часа после начала движения легковая машина догнала грузовик. Какое расстояние между посёлками?
Узнаем скорость сближения:
1) 80 - 60 = 20 ( км/ч ) - скорость сближения.
Узнаем расстояние между посёлками:
2) 20 * 2 = 40 ( км ) - расстояние между посёлками.
ответ:Сначала найдем саму функцию вида у=ax^2+bx+с, заменив переменные a, b и c числами. Для этого подставляем известные значения х и у:
а*0+b*0+с=4, отсюда находим с=4
a*1+b*1+4=-1, отсюда находим а=-5-b
(-5-b)*4+b*2+4=-4, отсюда находим b=-6 и подставляя это значение во второе уравнение находим, что a=1
Теперь ищем ее вершину:
По формуле вершин для парабол: х=-b/2a; y=(b^2-4ac)/4a, отсюда находим х=-((-6)/2*1)=3; у=-(((-6)^2-4*1*4)/(4*1))=-5
Альтернативно можно было бы решить через производную, результат бы не изменился.
ответ: координатой вершины является точка(3|-5).
Пошаговое объяснение:
Легковая машина догонит грузовик через 2 часа.
Обратная задача:Расстояние между посёлками - 40 кг.
Пошаговое объяснение:
Справка:
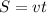
Исходная задача:Узнаем скорость сближения:
1) 80 - 60 = 20 ( км/ч ) - скорость сближения.
Узнаем время пути:
2) 40 : 20 = 2 ( ч ) - время пути.
Обратная задача:Условие:
Из посёлка A выехал легковой автомобиль со скоростью 80 км/ч, а из посёлка Б выехал грузовик со скоростью 60 км/ч. Через 2 часа после начала движения легковая машина догнала грузовик. Какое расстояние между посёлками?
Узнаем скорость сближения:
1) 80 - 60 = 20 ( км/ч ) - скорость сближения.
Узнаем расстояние между посёлками:
2) 20 * 2 = 40 ( км ) - расстояние между посёлками.