Через 4 часа моторная лодка встретится с плотом после выхода из пункта B.
Пошаговое объяснение:
Требуется найти, через какое время моторная лодка встретится с плотом после выхода из пункта B.
Плот проплывает расстояние между пунктами A и B за 20 часов. Такое же расстояние моторная лодка проплывает по озеру за 5 часов.
Вспомним формулы:
1. Пусть расстояние от А до В - S км.
Тогда скорость плота - Vтеч. = км/ч.
Заметим, что скорость плота равна скорости течения.
Собственная скорость лодки - Vл = км/ч.
⇒
Скорость лодки по течению:
Vпо теч. = Vл+Vтеч. = (км/ч)
Скорость лодки против течения:
Vпр.теч. = Vл - Vтеч. = (км/ч)
2. Рассмотрим движения из пункта А в пункт В.
Скорость плота - км/ч; скорость лодки по течению - км/ч
⇒ скорость лодки по течению в 5 раз больше, чем скорость плота.
То есть, когда лодка приплывет в пункт В, плот проплывет км и будет находиться в М.
3. Когда плот оказался в точке М, лодка развернулась и поплыла против течения со скоростью - км/ч.
Теперь можем считать, что одновременно навстречу друг другу выплыли плот и лодка соответственно из М и В, расстояние между которыми
(км)
Найдем искомое время до их встречи.
Для этого найдем скорость сближения:
Vc = Vп + Vпр.теч. = (км/ч)
4. Зная расстояние км и скорость км/ч, мы можем найти искомое время:
(ч).
12
1) S₁ = 2✓3 - площадь меньшего треугольника,
а₁=2 - катет, b₁ - катет, с₁- гипотенуза
S₁ = (a₁*b₁)/2
2S₁ = a₁*b₁
b₁ = 2S₁/a₁ = 2*2√3 /2 = 2√3
c₁ = √(a₁²+b₁²) = √(2²+(2√3)²) = √(4+12)=√16 = 4 - гипотенуза
2) Треугольники подобны
S₁ = 2✓3 S₂ = 18✓3
Площади подобных треугольников относятся как квадраты их соответствующих сторон, поэтому отношение площадей подобных треугольников равно квадрату коэффициента подобия.
k² = S₂ : S₁ = (18✓3) : (2✓3) = 9
k = ✓9 = 3 - коэффициент подобия треугольников
3) с₂ - гипотенуза большего треугольника
с₂ = k * c₁ = 3 * 4 = 12
Через 4 часа моторная лодка встретится с плотом после выхода из пункта B.
Пошаговое объяснение:
Требуется найти, через какое время моторная лодка встретится с плотом после выхода из пункта B.
Плот проплывает расстояние между пунктами A и B за 20 часов. Такое же расстояние моторная лодка проплывает по озеру за 5 часов.
Вспомним формулы:
1. Пусть расстояние от А до В - S км.
Тогда скорость плота - Vтеч. =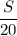 км/ч.
км/ч.
Заметим, что скорость плота равна скорости течения.
Собственная скорость лодки - Vл =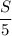 км/ч.
км/ч.
⇒
Скорость лодки по течению:
Vпо теч. = Vл+Vтеч. =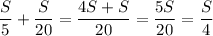 (км/ч)
(км/ч)
Скорость лодки против течения:
Vпр.теч. = Vл - Vтеч. =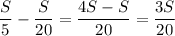 (км/ч)
(км/ч)
2. Рассмотрим движения из пункта А в пункт В.
Скорость плота -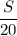 км/ч; скорость лодки по течению -
км/ч; скорость лодки по течению - 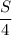 км/ч
км/ч
⇒ скорость лодки по течению в 5 раз больше, чем скорость плота.
То есть, когда лодка приплывет в пункт В, плот проплывет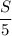 км и будет находиться в М.
км и будет находиться в М.
3. Когда плот оказался в точке М, лодка развернулась и поплыла против течения со скоростью -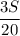 км/ч.
км/ч.
Теперь можем считать, что одновременно навстречу друг другу выплыли плот и лодка соответственно из М и В, расстояние между которыми
Найдем искомое время до их встречи.
Для этого найдем скорость сближения:
Vc = Vп + Vпр.теч. =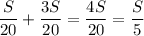 (км/ч)
(км/ч)
4. Зная расстояние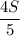 км и скорость
км и скорость 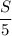 км/ч, мы можем найти искомое время:
км/ч, мы можем найти искомое время:
Через 4 часа моторная лодка встретится с плотом после выхода из пункта B.
12
Пошаговое объяснение:
1) S₁ = 2✓3 - площадь меньшего треугольника,
а₁=2 - катет, b₁ - катет, с₁- гипотенуза
S₁ = (a₁*b₁)/2
2S₁ = a₁*b₁
b₁ = 2S₁/a₁ = 2*2√3 /2 = 2√3
c₁ = √(a₁²+b₁²) = √(2²+(2√3)²) = √(4+12)=√16 = 4 - гипотенуза
2) Треугольники подобны
S₁ = 2✓3 S₂ = 18✓3
Площади подобных треугольников относятся как квадраты их соответствующих сторон, поэтому отношение площадей подобных треугольников равно квадрату коэффициента подобия.
k² = S₂ : S₁ = (18✓3) : (2✓3) = 9
k = ✓9 = 3 - коэффициент подобия треугольников
3) с₂ - гипотенуза большего треугольника
с₂ = k * c₁ = 3 * 4 = 12