Уравнение решается только в таком виде:
ОДЗ:
⇒
По свойствам логарифма степени: ,
Применяем свойство монотонности логарифмической функции:
каждое свое значение логарифмическая функция принимает ровно в
одной точке.
Поэтому если значения функции равны, то и аргументы равны:
или
не входит в ОДЗ
О т в е т. 3
Уравнение решается только в таком виде:
ОДЗ:
По свойствам логарифма степени: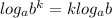 ,
, 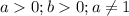
Применяем свойство монотонности логарифмической функции:
каждое свое значение логарифмическая функция принимает ровно в
одной точке.
Поэтому если значения функции равны, то и аргументы равны:
О т в е т. 3