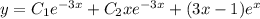Відповідь:
≈0,727
Покрокове пояснення:
позначимо х-продуктивність другого автомата
3х-продуктивність першого автомата
імовірність, що деталь проведена першим автоматом =3х/(3х+х)= 3/4=0,75
імовірність, що деталь проведена другим автоматом= х/(3х+х) =1/4=0,25
імовірність, що перший автомат справив деталь першого сорту=0,8 * 0,75=0,6
імовірність, що другий автомат справив деталь першого сорту=0,9 * 0,25=0,225
імовірність, що деталь першого сорту=0,6 + 0,225=0,825
імовірність, що на удачу взята деталь першого сорту проведена першим автоматом=0,6÷0,825≈0,727
Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного дифференциального уравнения, соответствующего данному неоднородному, и частного решения неоднородного дифференциального уравнения.
Решим однородное дифференциальное уравнение, соответствующее данному неоднородному:
Составим и решим характеристическое уравнение:
Запишем общее решение однородного уравнения:
Частное решение будем искать в виде:
Найдем первую и вторую производную:
Подставим значения функции и первых двух производных в исходное уравнение:
Сократим на :
Так как левая и правая часть равны, то коэффициенты при х и свободные члены также равны. Получаем систему:
Тогда частное решение имеет вид:
Общее решение заданного уравнения:
ответ:
Відповідь:
≈0,727
Покрокове пояснення:
позначимо х-продуктивність другого автомата
3х-продуктивність першого автомата
імовірність, що деталь проведена першим автоматом =3х/(3х+х)= 3/4=0,75
імовірність, що деталь проведена другим автоматом= х/(3х+х) =1/4=0,25
імовірність, що перший автомат справив деталь першого сорту=0,8 * 0,75=0,6
імовірність, що другий автомат справив деталь першого сорту=0,9 * 0,25=0,225
імовірність, що деталь першого сорту=0,6 + 0,225=0,825
імовірність, що на удачу взята деталь першого сорту проведена першим автоматом=0,6÷0,825≈0,727
Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного дифференциального уравнения, соответствующего данному неоднородному, и частного решения неоднородного дифференциального уравнения.
Решим однородное дифференциальное уравнение, соответствующее данному неоднородному:
Составим и решим характеристическое уравнение:
Запишем общее решение однородного уравнения:
Частное решение будем искать в виде:
Найдем первую и вторую производную:
Подставим значения функции и первых двух производных в исходное уравнение:
Сократим на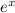 :
:
Так как левая и правая часть равны, то коэффициенты при х и свободные члены также равны. Получаем систему:
Тогда частное решение имеет вид:
Общее решение заданного уравнения:
ответ: