Введём следующие обозначения. Обозначим вершины треугольника как A, B, C, причём AB : BC : AC = m : n : p. Обозначим точки касания с AB как M, с BC — N, AC — P, отрезки касательных AM = AP = x, BM = BN = y, CN = CP = z (отрезки касательных, проведённых из одной точки, равны).
Из отношения AB : BC : AC = m : n : p следует, что AB = mk, BC = nk, AC = pk. Тогда получаем
Вычтем из третьего уравнения второе и запишем его в системе с первым:
Подставим найденный x в третье уравнение и выразим z: .
Пошаговое объяснение:
Введём следующие обозначения. Обозначим вершины треугольника как A, B, C, причём AB : BC : AC = m : n : p. Обозначим точки касания с AB как M, с BC — N, AC — P, отрезки касательных AM = AP = x, BM = BN = y, CN = CP = z (отрезки касательных, проведённых из одной точки, равны).
Из отношения AB : BC : AC = m : n : p следует, что AB = mk, BC = nk, AC = pk. Тогда получаем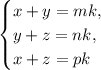
Вычтем из третьего уравнения второе и запишем его в системе с первым: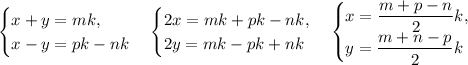
Подставим найденный x в третье уравнение и выразим z: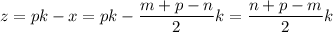 .
.
Тогда искомые отношения: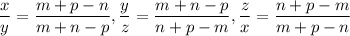
Решение задачи:
1. Для решения задачи найдем сколько времени был в пути автомобиль проехав 300 километров со скоростью 60 километров в час.
300/60=5 часов
2. Определим за какое время автомобиль проехал следующие 300 километров двигаясь со скоростью 100 километров в час.
300/100=3 часа
3. Находим время последнего пути автомобиля.
300/75=4 часа
4. Вычислим сколько часов был в пути автомобиль.
5+3+4=12 часов
5. Найдем пройденный путь за 12 часов.
300+300+300=900 километров
6. Найдем среднюю скорость автомобиля на протяжении всего пути.
900/12=75 километров в час.
ответ: Средняя скорость автомобиля семьдесят пять километров в час.