Знайти площу криволінійної трапеції (А) і об'єм тіла обертання (Б)

Найти площадь криволинейной трапеции (А) и объем тела вращения (Б). Фото ниже

Показать ответ

Ответ:

alii333

06.08.2022 00:36

Задача 3Пусть anan будет арифметической прогрессией, для которой a1=15a1=15 и d=3d=3. Найдите сумму первых десяти членов.Задача 4Пусть anan будет арифметической прогрессией, для которой a3=13a3=13 и a11=25a11=25. Найдите a7a7Задача 5Найдите разницу арифметической прогрессии anan, если a5=18a5=18 и a2=9a2=9Задача 6Пусть anan есть арифметическая прогрессия, для которой a2=5a2=5 и a1=−11a1=−11. Найдите разницу прогрессии dd.Задача 7Пусть anan есть арифметической прогрессией, для которой a1=1a1=1 и d=1d=1. Найдите a1083a1083Задача 8Пусть anan есть арифметической прогрессией. Если a1=15a1=15 и a2=8a2=8, определите a19a19.Задача 9Пусть anan есть арифметической прогрессией, для которой d=12d=12 и a3=43a3=43. Найдите a1a1Задача 10Пусть anan есть арифметической прогрессией. Если a1=7a1=7 и d=4d=4, определите сумму первых 6 элементов с чётными индексами.

0,0(0 оценок)

Ответ:

AlinkaMakovka

19.11.2022 11:44

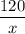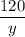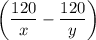Пусть скорость автобуса равна х км/ч, а скорость легковой машины - у км/ч. По условию, y - x = 12. Тогда время затраченное автобусом равно $\dfrac{120}{x}$ , а легковым автомобилем - $\dfrac{120}{y}$ на весь путь время затрачено $\left(\dfrac{120}{x}-\dfrac{120}{y}\right)$ часов. Зная, что легковая машина пришла в город В на 5 мин раньше, чем автобус, составим систему уравнений

$\displaystyle \begin{cases}&\text{}y-x=12\\&\text{}\dfrac{120}{x}-\dfrac{120}{y}=\dfrac{15+5}{60}\end{cases}~~~\Rightarrow~~~\begin{cases}&\text{}y=x+12\\&\text{}\dfrac{120}{x}-\dfrac{120}{x+12}=\dfrac{1}{3}\end{cases}$