Один из показателей степени числа 3 может быть представлен в виде . Поэтому одно из представленных чисел может быть членом данной геометрической прогрессии - это число .
Можно представить заданную прогрессию таким образом :
Один из показателей степени числа 3 может быть представлен в виде . Поэтому одно из представленных чисел может быть членом данной геометрической прогрессии - это число
. Поэтому одно из представленных чисел может быть членом данной геометрической прогрессии - это число 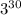 .
.
Можно представить заданную прогрессию таким образом :