1.Функция задана формулой у = 3х ‒ 15. Определите:
а) значение функции соответствующее значению аргумента равному 2,5;
б) значение аргумента, при котором значение функции равно 6;
в) проходит ли график функции через точку А (-3;24).
2.Постройте график функции у = 1,5х + 3. Укажите с графика
а) чему равно значение у, при х= ‒ 2.
б) чему равно значение х, при котором у = 6.
3.В одной и той же системе координат постройте графики функций:
а) у = 3х; б) у = 3; в) у = х+3.
4.Найдите координаты точек пересечения графиков функций у = ‒ 40х+3 и у= ‒ 24х + 11.
5.Задайте формулой линейную функцию, график которой параллелен прямой
у= ‒ 3,5х + 8 и проходит через начало координат.
6.Найдите координаты точек пересечения графика функции у = 5х + 5 с осями координат.
Объяснение:
4 часа 30 мин=270мин
6 часов 45 мин=405мин
1/270 часть бассейна нальет первый кран за 1 мин
1/405 часть бассейна нальет второй кран за 1 мин
1/405+1/270=5/810=1/162 часть бассейна нальют 2 крана за 1 мин
1:(1/162)=162 мин - время за которое 2 крана наполнят весь бассейн
первый кран был открыт 162 мин
162/270=3/5 - бассейна наполнит первый кран за 162 мин1-3/5=2/5 бассейна нужно наполнить второму крану
2/5 : 1/405=2*405/5*1=810/5=162 мин - Через столько времени бассейн наполнится.
ответ:162 мин. 1-3/5=2/5 бассейна нужно наполнить второму крану
2/5 : 1/405=2*405/5*1=810/5=162 мин - Через столько времени бассейн наполнится.
ответ:162 мин.
Объяснение:
y = -x
1) Функция имеет единственный ноль к точке (0, 0)
2) Область определения функции ( -∞ ; +∞)
3) Область значений такая же, т.е. ( -∞ ; +∞)
4) Область определения совпадает с областью значений
5) Функция располагается в 2 и 4 четвертях
6) Функция положительна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент отрицателен
7) Функция отрицательна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент положителен
8) Это монотонно убывающая функция
9) Функция убывает на всей своей области определения
10) Функция не имеет периода
11) График этой функции - прямая, проходящая через центр координат
12) Это нечётная функция
13) Тангенс угла наклона касательной к точке графика постоянен и равен -1 для всех х
14) Площадь под графиком от 0 до х равна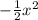
Здесь все свойства функции, выбирайте нужные.
На графике красным - сам график
Голубым подписаны четверти, их подписывать не обязательно.