100ballow 1. Дана последовательность:

a) Запишите формулу общего члена последовательности.

b) Напишите следующие два члена последовательности.

с) Ученик утверждает, что 1/15 является членом данной последовательности.

Прав ли ученик? Обоснуйте свой ответ. [4]​

1)x-y=2

xy=3

Делаем методом постановки

x=2+y

xy=3

x=2+y

y×(2+y)=3

x=2+y

y²+2y-3=0

y²+2y-3=0

За теоремой Виета

y=-3;y=1

x=2+y

y=-3:y=1

x=2-3;x=2+1

y=-3;y=1

x=-1;x=3

y=-3;y=1

(-1;-3)(3;1)

2)x-y=3

xy=4

Делаем методом постановки

x=3+y

xy=4

x=3+y

y(3+y)=4

x=3+y

y²+3y-4=0

y²+3y-4=0

За теоремой Виета

y=-4;y=1

x=3+y

y=-4;y=1

x=3-4;x=3+1

y=-4;y=1

x=-1;x=4

y=-4;y=1

(-1;-4);(4;1)

3)2x²-y²=46

xy=10

Метод постановки

2x²-y²=46

y=10/x

2x²-100/x²=46

y=10/x

2x^4-100-46x²/x²=0|×x²

y=10/x

2x^4-46x²-100=0|:2

y=10/x

x^4-23x²-50=0

y=10/x

x^4-23x²-50=0

Замена

Пусть x²=t, тогда:

t²-23t-50=0

За теоремой Виета

t=-2;t=25

x²=-2—такого не существует;x²=25

x²=25

x=5 или x=-5

x=5;x=-5

y=10/x

x=5;x=-5

y=10/5;y=10/-5

x=5;x=-5

y=2, y=-2

(5;2);(-5;-2)

от -∞ до -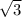 функция убывает;

от -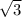 до 0 функция возрастает;

от 0 до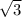 функция убывает;

от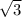 до ∞ функция возрастает;

Объяснение:

в точках экстремума первая производная функции равна нулю.

Найдём эти точки, для этого возьмём первую производную.

y'=4x^3-12x;

приравняем к нулю.

4x^3-12x=0;

x^3-3x=0;

x(x^2-3)=0;

x1=0;

x2=;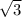

x3=-;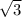

Теперь возьмём вторую производную функции в этих точках.

y''=12x^2-12;

y''(x1)=-12 (меньше нуля, значит это точка максимума)

y''(x2)=12*3-12 (больше нуля, значит это точка минимума)

y''(x3)=12*3-12 (больше нуля, значит это точка минимума)

от -∞ до -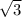 функция убывает;

от -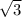 до 0 функция возрастает;

от 0 до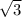 функция убывает;

от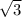 до ∞ функция возрастает;