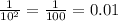мы можем записать это дробью, чтобы было легче вычислять.
при одинаковых основаниях (одинаковых больших буквах или цифрах) мы можем сложить степени, если мы перемножаем числа. также можем вычитать их, если числа делим, то бишь 14+9=23. получилось . теперь мы имеем такую дробь: . дробную черту можно заменить делением, а значит степени можно вычесть. не пугайтесь, что мы вычитаем из большего меньшее. теперь мы имеем следующее: . минусовую степень мы переворачиваем, получаем обыкновенную дробь. в числитель ставим единицу, а вниз - число в степени: . дальше всё просто: подставляем число и решаем.
1) 2cosx-1 < 0
cosx < 1/2
arccos(1/2) + 2πn < x < 2π - arccos(1/2) + 2πn, n ∈ Z
π/3 + 2πn < x < 2π - π/3 + 2πn, n ∈ Z
π/3 + 2πn < x < 5π/3 + 2πn, n ∈ Z
2) sin2x - √2/2 < 0
sin2x < √2/2
- π - arcsin(√2/2) + 2πk < 2x < arcsin(√2/2) + 2πk, k ∈ Z
- π - π/4 + 2πk < 2x < π/4 + 2πk, k ∈ Z
- 5π/4 + 2πk < 2x < π/4 + 2πk, k ∈ Z
- 5π/8 + πk < x < π/8 + πk, k ∈ Z
3) tgx<1
- π/2 + πn < x < arctg(1) + πn, n ∈ Z
- π/2 + πn < x < π/4 + πn, n ∈ Z
мы можем записать это дробью, чтобы было легче вычислять.
при одинаковых основаниях (одинаковых больших буквах или цифрах) мы можем сложить степени, если мы перемножаем числа. также можем вычитать их, если числа делим, то бишь 14+9=23. получилось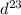
. теперь мы имеем такую дробь: 
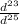. дробную черту можно заменить делением, а значит степени можно вычесть. не пугайтесь, что мы вычитаем из большего меньшее. теперь мы имеем следующее: 
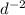. минусовую степень мы переворачиваем, получаем обыкновенную дробь. в числитель ставим единицу, а вниз - число в степени: 
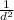. дальше всё просто: подставляем число и решаем. 