Продолжаем изучение раздела «Функции и графики», и следующая станция нашего путешествия – Область определения функции. Активное обсуждение данного понятия началось в статье о множествах и продолжилось на первом уроке о графиках функций, где я рассмотрел элементарные функции, и, в частности, их области определения. Поэтому чайникам рекомендую начать с азов темы, поскольку я не буду вновь останавливаться на некоторых базовых моментах.
Предполагается, читатель знает область определения следующих функций: линейной, квадратичной, кубической функции, многочленов, экспоненты, синуса, косинуса. Они определены на (множестве всех действительных чисел). За тангенсы, арксинусы, так и быть, прощаю =) – более редкие графики запоминаются далеко не сразу.
Область определения – вроде бы вещь простая, и возникает закономерный вопрос, о чём же будет статья? На данном уроке я рассмотрю распространённые задачи на нахождение области определения функции. Кроме того, мы повторим неравенства с одной переменной, навыки решения которых потребуются и в других задачах высшей математики. Материал, к слову, весь школьный, поэтому будет полезен не только студентам, но и учащимся. Информация, конечно, не претендует на энциклопедичность, но зато здесь не надуманные «мёртвые» примеры, а жареные каштаны, которые взяты из настоящих практических работ.
Начнём с экспресс-вруба в тему. Коротко о главном: речь идёт о функции одной переменной . Её область определения – это множество значений «икс», для которых существуют значения «игреков». Рассмотрим условный пример:
Продолжаем изучение раздела «Функции и графики», и следующая станция нашего путешествия – Область определения функции. Активное обсуждение данного понятия началось в статье о множествах и продолжилось на первом уроке о графиках функций, где я рассмотрел элементарные функции, и, в частности, их области определения. Поэтому чайникам рекомендую начать с азов темы, поскольку я не буду вновь останавливаться на некоторых базовых моментах.
Предполагается, читатель знает область определения следующих функций: линейной, квадратичной, кубической функции, многочленов, экспоненты, синуса, косинуса. Они определены на (множестве всех действительных чисел). За тангенсы, арксинусы, так и быть, прощаю =) – более редкие графики запоминаются далеко не сразу.
Область определения – вроде бы вещь простая, и возникает закономерный вопрос, о чём же будет статья? На данном уроке я рассмотрю распространённые задачи на нахождение области определения функции. Кроме того, мы повторим неравенства с одной переменной, навыки решения которых потребуются и в других задачах высшей математики. Материал, к слову, весь школьный, поэтому будет полезен не только студентам, но и учащимся. Информация, конечно, не претендует на энциклопедичность, но зато здесь не надуманные «мёртвые» примеры, а жареные каштаны, которые взяты из настоящих практических работ.
Начнём с экспресс-вруба в тему. Коротко о главном: речь идёт о функции одной переменной . Её область определения – это множество значений «икс», для которых существуют значения «игреков». Рассмотрим условный пример:
Объяснение:
№1
1) a¹³*a⁻¹⁶=a¹³⁽⁻¹⁶⁾ = a¹³⁻¹⁶=a⁻³
-3⁻³ =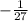
2) a⁻⁹:a⁻⁸=a⁻⁹⁻⁽⁻⁸⁾ = a⁻⁹⁺⁸ = a⁻¹
3) (a⁻²)¹¹*a²⁰= a⁽⁻²⁾°¹¹ * a²⁰ = a⁻²² * a²⁰ = a⁻²²⁺²⁰= a⁻²
1 - Б
2 - А
3 - В
№2
График, думаю, сами легко построите.
y = 8/x
1) Значение функции, если x = -4
y = 8/-4 = -2
2) Значение аргумента, если y = 1
x = 8/y
x = 8/1 = 8
3) Аргумент принимает отрицательные значения, если x ∈ (-∞, 0)
№3
______
Область допустимых значений (Условие):
x-5 ≠ 0
x ≠ 5
_______
Если знаменатели равны, то и числители тоже равны.
2x -9 = 3x - 14
2x - 3x = -14 + 9
-x = -5
x = 5 - не подходит по ОДЗ
x ∈ ∅