Докажите, что число 4n^4+1 только при n=1 является - вопрос №4411327617 от Inna14888 15.05.2021 19:37

Question

Алгебра: Докажите, что число 4n^4+1 только при n=1 является простым, а при всех остальных натуральных n составное

Inna14888 · Answer

При n=1: 4n^4+1=4*1^4+1=5 - простое число

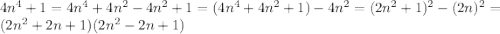При n>1: 4n^4+1= 4n^4+4n^2-4n^2+1=(4n^4+4n^2+1)-4n^2= (2n^2+1)^2-(2n)^2=(2n^2+2n+1)(2n^2-2n+1) - сложное число так как каждый из множителей

2n^2+2n+1>2*1+2*1+1=5>1

2n^2-2n+1=2n(n-1)+1>1

Доказано