ответ: является тождеством.
Объяснение: Начнем с левой стороны.
Применим правило произведения к ab.
Умножим a^(-1) на a^2, складывая показатели степеней.
Упростим .
Переместим b^(-3) в числитель, используя правило отрицательных степеней .
Умножим b^2 на b^3, складывая показатели степеней.
Перемножаем степени в .
Умножим b^5 на b^(-9), складывая показатели степеней.
является тождеством.
Поскольку обе части эквивалентны, уравнение является тождеством.
Объяснение:
a^-1*a^2*b^2*b^-9:b^-3=a^(-1+2)*b^(2-9+3)=a*b^-4 при делении показатели вычитаются-7-(-3)=-7+3=-4
ответ: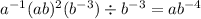 является тождеством.
является тождеством.
Объяснение: Начнем с левой стороны.
Применим правило произведения к ab.
Умножим a^(-1) на a^2, складывая показатели степеней.
Упростим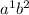 .
.
Переместим b^(-3) в числитель, используя правило отрицательных степеней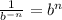 .
.
Умножим b^2 на b^3, складывая показатели степеней.
Перемножаем степени в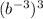 .
.
Умножим b^5 на b^(-9), складывая показатели степеней.
Поскольку обе части эквивалентны, уравнение является тождеством.
Объяснение:
a^-1*a^2*b^2*b^-9:b^-3=a^(-1+2)*b^(2-9+3)=a*b^-4 при делении показатели вычитаются-7-(-3)=-7+3=-4