Имеется набор цифр: 0, 1, 2, 3, 4, 5. 1)Сколько различных четырёхзначных чисел (без повторения цифр) можно составить
из этого набора при условии, что числа будут чётными?
2) Сколько различных четырёхзначных чисел (без повторения цифр) можно составить
из этого набора при условии, что числа будут кратными 5?
Чтобы изобразить график линейной функции вида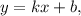
где 
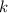и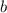 
— коэффициенты, достаточно на координатной плоскости отметить две точки и провести через них прямую.
Для этого строят таблицу для двух точек: первая строка — абсцисса (иксы), вторая строка — ордината (игреки). Вы — хозяин своей таблицы. Подбирайте любое значение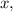
подставляйте его в функцию и находите 
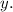(Подбирайте числа в пределах разумного.)
Пример. Изобразить график линейной функции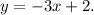
Строим таблицу для двух точек:
Пусть
Тогда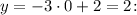
Пусть
Тогда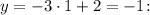
Имеем заполненную таблицу для двух точек. Изобразим координатную плоскость, отметим две точк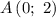и:
и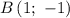 
— и проведем через них прямую (см. вложение). График линейной функции 
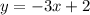построен.
х=54, у=2
х=24, у=8
Объяснение:
Выразим х через у:
х= (243у)/(у+1)²
243 делится нацело на 3, 9, 27, 81 , из этих чисел только 9 и 81 есть полными квадратами. Подставляем: (у+1)² = 9;
у+1 = 3;
у = 2
Находим х при у=2 х = (243*2)/9 = 54
Первое решение: х=54; у=2
Подставляем: (у+1)² = 81;
у+1 = 9;
у = 8
Находим х при у = 8 х = (243*8)/81 = 24
Второе решение: х=24; у=8
ПРОВЕРКА: 1) 54*(2+1)² = 243*2; 2) 24*(8+1)² = 243*8
54*9 = 486; 24*81 = 1944
486 = 486 1944=1944