Объяснение:
здесь надо рассмотреть два случая
1) х-5>0, x>5, тогда |x-5|=x-5 и 1/(х-5) -2<0, (1-2x+10)/(x-5) <0,
(11-2x)/(x-5) <0 , - __(5)+___(5,5)___-___
общее решение x>5,5 (с учетом, что x-5>0)
2) x-5<0, x<5, тогда |x-5|=5-x и получим уравнение:
1/(5-x) -2<0, (1-10+2x)/ (5-x) <0, (2x-9)/ (5-x) <0
-___(4,5)+(5)___- и общее решение
x<4,5 (с учетом, что x-5<0) , объединяем два случая и
ответ: (-Б; 4,5) и (5,5; +Б) (Б- бесконечность)
Правильное условие такое:
У брата х груш, а у сестры у² яблок. Вместе у них было 11 этих фруктов. Если бы у брата было у груш, а у сестры -х² яблок, то всего этих фруктов у них было бы 7. Сколько было груш и сколько было яблок?
Решение.
ОДЗ:
Методом подбора быстрее.
1) Начнем с решения второго уравнения.
Если то 7-1=6. Тогда не натуральное число.
Если то 7-2=5. Тогда не натуральное число.
Если то 7-3=4. Тогда натуральное число.
Получили решение
2) Подставим в первое уравнение .
верное равенство.
ответ: 2 груши у брата;
3 яблока у сестры.
Объяснение:
здесь надо рассмотреть два случая
1) х-5>0, x>5, тогда |x-5|=x-5 и 1/(х-5) -2<0, (1-2x+10)/(x-5) <0,
(11-2x)/(x-5) <0 , - __(5)+___(5,5)___-___
общее решение x>5,5 (с учетом, что x-5>0)
2) x-5<0, x<5, тогда |x-5|=5-x и получим уравнение:
1/(5-x) -2<0, (1-10+2x)/ (5-x) <0, (2x-9)/ (5-x) <0
-___(4,5)+(5)___- и общее решение
x<4,5 (с учетом, что x-5<0) , объединяем два случая и
ответ: (-Б; 4,5) и (5,5; +Б) (Б- бесконечность)
Правильное условие такое:
У брата х груш, а у сестры у² яблок. Вместе у них было 11 этих фруктов. Если бы у брата было у груш, а у сестры -х² яблок, то всего этих фруктов у них было бы 7. Сколько было груш и сколько было яблок?
Решение.
ОДЗ: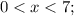
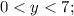
Методом подбора быстрее.
1) Начнем с решения второго уравнения.
Если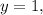 то 7-1=6. Тогда
то 7-1=6. Тогда 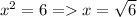 не натуральное число.
не натуральное число.
Если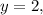 то 7-2=5. Тогда
то 7-2=5. Тогда 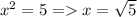 не натуральное число.
не натуральное число.
Если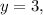 то 7-3=4. Тогда
то 7-3=4. Тогда 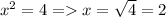 натуральное число.
натуральное число.
Получили решение
2) Подставим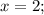
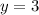 в первое уравнение
в первое уравнение 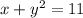 .
.
ответ: 2 груши у брата;
3 яблока у сестры.