Объяснение:
1)Пусть боковая сторона равна x см, тогда основание равно y см. Зная, что основание на 7 больше, составлю первое уравнение системы:
y-x = 7
Зная, что периметр равнобедренного треугольника равен 43 см(для равнобедренного треугольника получаем выражение 2x + y), составлю второе уравнение системы:
2x + y = 43
Таким образом, получаем следующую систему уравнений:
2x+y = 43
решу систему методом подстановки:
y = x+7
2x + x+7 = 43 (1)
(1)2x+x+7 = 43
3x+7 = 43
3x = 36
x = 12
12 см - боковая сторона треугольника, но надо всё равно дорешать систему.
y = 12+7 = 19
ответ, 12 см равна боковая сторона. ответ на вопрос задачи мы получили.
Для решения запишем формулу бинома Ньютона:
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение .
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение .
Рассмотрим многочлен , где:
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена :
- степень определяется выражением , то есть степень равна 84
- свободный член равен
- степень определяется выражением , то есть степень равна 6
Наконец, для многочлена получим:
- степень определяется выражением , то есть степень равна 90
Сумма степени и свободного члена многочлена :
ответ: 98
Объяснение:
1)Пусть боковая сторона равна x см, тогда основание равно y см. Зная, что основание на 7 больше, составлю первое уравнение системы:
y-x = 7
Зная, что периметр равнобедренного треугольника равен 43 см(для равнобедренного треугольника получаем выражение 2x + y), составлю второе уравнение системы:
2x + y = 43
Таким образом, получаем следующую систему уравнений:
y-x = 7
2x+y = 43
решу систему методом подстановки:
y = x+7
2x + x+7 = 43 (1)
(1)2x+x+7 = 43
3x+7 = 43
3x = 36
x = 12
12 см - боковая сторона треугольника, но надо всё равно дорешать систему.
x = 12
y = 12+7 = 19
ответ, 12 см равна боковая сторона. ответ на вопрос задачи мы получили.
Для решения запишем формулу бинома Ньютона:
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение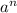 .
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение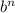 .
.
Рассмотрим многочлен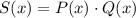 , где:
, где:
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена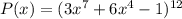 :
:
- степень определяется выражением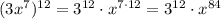 , то есть степень равна 84
, то есть степень равна 84
- свободный член равен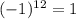
Для многочлена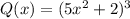 :
:
- степень определяется выражением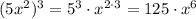 , то есть степень равна 6
, то есть степень равна 6
- свободный член равен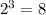
Наконец, для многочлена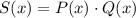 получим:
получим:
- степень определяется выражением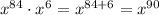 , то есть степень равна 90
, то есть степень равна 90
- свободный член равен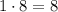
Сумма степени и свободного члена многочлена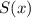 :
:
ответ: 98