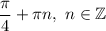Найдите область определения функции y= если область значений: 1) [0;4]; 2) [0,04;1]; 3) [25; 225]?​

1,75

Объяснение:

S = x1(1-x2) + x2(1-x3) + x3(1-x4) + x4(1-x5) + x5(1-x6) + x6(1-x7) + x7(1-x1)

При условии: x1; x2; x3; x4; x5; x6; x7 ∈ [0; 1]

Очевидно, что при x1 = x2 = x3 = x4 = x5 = x6 = x7 = 0 будет S = 0

Точно также, при x1 = x2 = x3 = x4 = x5 = x6 = x7 = 1 будет S = 0

Так как выражение симметрично относительно переменных, то любую переменную можно заменить на любую другую.

Это значит, что максимум будет достигнут при равных значениях всех переменных.

Сумма будет максимальной при x1 = x2 = x3 = x4 = x5 = x6 = x7 = 0,5

S = 0,5*0,5 + 0,5*0,5 + 0,5*0,5 + 0,5*0,5 + 0,5*0,5 + 0,5*0,5 + 0,5*0,5 =

= 0,25*7 = 1,75

Воспользуемся формулой разности кубов:

Выносим за скобки общий множитель:

Уравнение распадается на два. Решаем первое:

Почленно разделим на :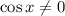

Решаем второе уравнение:

Заметим в левой части основное тригонометрическое тождество:

Обе части уравнения домножим на 2:

Чтобы в левой части применить формулу синуса двойного угла:

Но так как синус любого угла принимает значения только из отрезка от -1 до 1, то последнее уравнение не имеет решение.

Значит, никаких других корней, кроме найденных ранее, исходное уравнение не имеет.

ответ: