Область определения функции обычно обозначают большой буквой
Д ( писанной) . Мы будем пользоваться международным обозначением D (y)- частным случаем от написания D(f) ( Вы пишпите как у вас требуют, если Россия, то большая прописная буква Д).
Так как знаменатель не может быть равен нулю , то мы должны найти нули в знаменателе и исключить их из области определения.
х²+2х≠0;
х(х+2)≠0; ( тут рассуждаем, что произведение равно0, когда один из множителей равен 0)
х₁≠0 или х₂+2≠0
х₂≠-2.
( Мы нашли нули функции теперь запишем область определения функции : это любое значение от -∞ до +∞, кроме -2 и 0,( можно нарисовать прямую и отметить эти две точки пустыми кружочками) что математически запишем)
ответ : D(y)=(-∞ ; -2) ∪ ( -2; 0) ∪ (0; +∞)
2) Рассуждения те же: перед нами дробь- знаменатель не может быть равен 0, что и запишем.
7-х²≠0
-х²≠ -7
х²≠7
х₁ ≠√7 х₂≠ -√7
ответ: D(y)=(-∞ ; -√7) ∪ ( -√7; √7) ∪ ( √7; +∞)
3) знаменатель не может быть равен 0, что и запишем.
5х²+0,6≠0
5х²≠ -0,6- тут останавливаемся и рассуждаем, что квадрат числа никогда не может быть отрицательным , поэтому нет таких значений х, при котором данный знаменатель мог бы быть равен 0
ответ: D(y)=(-∞; +∞)
! иногда ещё пишут D(y) ∈ R ( читается область определения функции- любое число)
4) опять рассуждаем , что знаменатель не может быть равен 0
Объяснение:
1
x²+2x≠0
x(x+2)≠0
x₁≠0
x+2≠0
x≠ -2
x є (-∞;-2) υ (-2;0) υ (0;+∞)
2)
7-х²≠0
-х²≠ -7
х²≠7
х≠±√7
x є (-∞;-√7) υ (-√7;√7) υ (√7;+∞)
3
5х²+0,6≠0
5х²≠ -0,6
х²≠ -0,6:5
х²≠ -0,12
х є R
х є (-∞;+∞)
множество всех действительных чисел, потому что знаменатель никогда не будет равен 0
4)
9х-4,5≠0
9х≠4,5
х≠4,5:9
х≠0,5
x є (-∞;0,5) υ (0,5;+∞)
1) D(y)=(-∞ ; -2) ∪ ( -2; 0) ∪ (0; +∞) ;
2) D(y)=(-∞ ; -√7) ∪ ( -√7; √7) ∪ ( √7; +∞) ;
3) D(y)=(-∞; +∞) ;
4) D(y)=(-∞; 0,5) ∪(0,5; +∞)
1)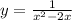
Область определения функции обычно обозначают большой буквой
Д ( писанной) . Мы будем пользоваться международным обозначением D (y)- частным случаем от написания D(f) ( Вы пишпите как у вас требуют, если Россия, то большая прописная буква Д).
Так как знаменатель не может быть равен нулю , то мы должны найти нули в знаменателе и исключить их из области определения.
х²+2х≠0;
х(х+2)≠0; ( тут рассуждаем, что произведение равно0, когда один из множителей равен 0)
х₁≠0 или х₂+2≠0
х₂≠-2.
( Мы нашли нули функции теперь запишем область определения функции : это любое значение от -∞ до +∞, кроме -2 и 0,( можно нарисовать прямую и отметить эти две точки пустыми кружочками) что математически запишем)
ответ : D(y)=(-∞ ; -2) ∪ ( -2; 0) ∪ (0; +∞)
2) Рассуждения те же: перед нами дробь- знаменатель не может быть равен 0, что и запишем.
7-х²≠0
-х²≠ -7
х²≠7
х₁ ≠√7 х₂≠ -√7
ответ: D(y)=(-∞ ; -√7) ∪ ( -√7; √7) ∪ ( √7; +∞)
3) знаменатель не может быть равен 0, что и запишем.
5х²+0,6≠0
5х²≠ -0,6- тут останавливаемся и рассуждаем, что квадрат числа никогда не может быть отрицательным , поэтому нет таких значений х, при котором данный знаменатель мог бы быть равен 0
ответ: D(y)=(-∞; +∞)
! иногда ещё пишут D(y) ∈ R ( читается область определения функции- любое число)
4) опять рассуждаем , что знаменатель не может быть равен 0
9х-4,5≠0;
9х≠4,5;
х≠4,5:9;
х≠0,5
ответ :D(y)=(-∞; 0,5) ∪(0,5; +∞)