Оцени погрешность приближённого равенства:
√5≈2,24.
Отметь один вариант ответа:

|2,24−√5|

√5−2,24

2,24−√5

|√5−2,24|
​

(см. объяснение)

Объяснение:

Первый :

Рассмотрим функцию .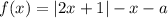

Тогда уравнение примет вид .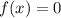

Заметим, что решающую роль на поведение функции (ее возрастание или убывание) всегда оказывает знак при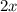 . Тогда функция убывает на промежутке , а возрастает на 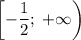. Значит единственное решение достигается тогда и только тогда, когда .

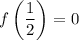Получили уравнение:

Итого при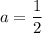 исходное уравнение имеет единственное решение.

Второй :

Построим график этого уравнения в координатах :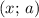

(см. прикрепленный файл)

Тогда ответом будет .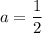

Третий :

Знаем, что при :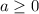

Тогда единственное решение возможно, только если .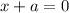

Получили уравнение:

Так как .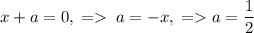

Задание выполнено!

-62

Объяснение:

f(x)=ax²+bx+c

Определим коэффициенты a, b, с.

1) Коэффициент а находим по формуле y=a(x-m)²+n, где (m;n) - координаты вершины параболы, а (х;у) - координата любой точки параболы, например, (1;1).

m=2; n=2

a(1-2)²+2=1

a(-1)²=-1

a*1=-1

a=-1

2) Коэффициент b находим из формулы для вершины параболы:

  -b/2a = m

  b = -m*2a =-2*2*(-1)=4

3) Коэффициент с найдём как ординату пересечения параболы с осью Оу. Искомая точка (0;-2), значит, с=-2

4) Запишем уравнение параболы: f(x) = -x²+4x-2

5) Находим f(10):

f(10)= -10²+4*10-2 = -100+40-2 = -62