a)
Область допустимых значений
(т. к. на нуль делить нельзя)
рассмотрим числитель
рассмотрим знаменатель
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
следовательно и
ответ: при ; данное выражение равно нулю.
б)
корнем этого уравнения является, что
ответ: при данное выражение равно нулю.
в)
Заметим, что данное выражение можно свернуть в квадрат
Cледовательно уравнение имеет один корень:
дана функция f(x)=x^3+3x^2
уравнение касательной к графику функции в точке а:
y(a) = f(a)+f'(a)(x-a)
Это уравнение прямой с угловым коэффициентом f'(a) (т.е. это тангенс угла наклона прямой к оси абцисс)
Условие параллельности оси абцисс: угол равен 0, следовательно, и его тангенс 0, следовательно и f'(a)=0. а - искомые точки
Берём производную: f' (x) = 3x^2+6x, приравниваем к нулю и решаем полученное уравнение относительно x:
3x^2+6x=0
x1=0
x2=2
Эти точки и есть искомые
Теперь напишем касательные:
в точке x1=0 касательная В ТОЧНОСТИ СОВПАДАЕТ С ОСЬЮ АБЦИСС
в точке x2=2 y= f(2)+0*(x-2) = 8- 3*4 = -4
это прямая y=-4
a)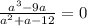
Область допустимых значений
рассмотрим числитель
рассмотрим знаменатель
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
следовательно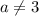 и
и 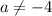
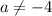
ответ: при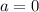 ;
; 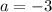 данное выражение равно нулю.
данное выражение равно нулю.
б)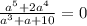
Область допустимых значений
рассмотрим числитель
рассмотрим знаменатель
корнем этого уравнения является, что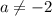
ответ: при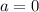 данное выражение равно нулю.
данное выражение равно нулю.
в)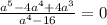
Область допустимых значений
рассмотрим числитель
Заметим, что данное выражение можно свернуть в квадрат
Cледовательно уравнение имеет один корень:
рассмотрим знаменатель
ответ: при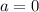 данное выражение равно нулю.
данное выражение равно нулю.
дана функция f(x)=x^3+3x^2
уравнение касательной к графику функции в точке а:
y(a) = f(a)+f'(a)(x-a)
Это уравнение прямой с угловым коэффициентом f'(a) (т.е. это тангенс угла наклона прямой к оси абцисс)
Условие параллельности оси абцисс: угол равен 0, следовательно, и его тангенс 0, следовательно и f'(a)=0. а - искомые точки
Берём производную: f' (x) = 3x^2+6x, приравниваем к нулю и решаем полученное уравнение относительно x:
3x^2+6x=0
x1=0
x2=2
Эти точки и есть искомые
Теперь напишем касательные:
в точке x1=0 касательная В ТОЧНОСТИ СОВПАДАЕТ С ОСЬЮ АБЦИСС
в точке x2=2 y= f(2)+0*(x-2) = 8- 3*4 = -4
это прямая y=-4