В первом уравнении мы раскрыли модуль: при x > 0 уравнение имеет вид y + a = 1, при x ≤ 0 оно не определено.
График первого уравнения - прямая, параллельная оси Ox, которая определена при x > 0. График второго уравнения - парабола, её вершина имеет координаты (-a; -3). При движении прямой вниз парабола сдвигается влево, а при движении прямой вверх - вправо.
Система имеет одно решение, если прямая касается параболы или парабола пересекает её один раз.
1 случай. Касание. Прямая, которая касается параболы, имеет уравнение y = -3 ⇒ 1 - a = -3 ⇔ a = 4. Но тогда вершина параболы будет иметь координату (-4; -3), а при x < 0 первое уравнение не определено. a = 4 не подходит.
2 случай. Пересечение. Если бы прямая y = 1 - a была определена в точке x = 0, то парабола имела бы одно пересечение с прямой в некой точке (0; y₁), двигалась вправо, пока её левая ветвь вновь не пересекла прямую в точке (0; y₂). Но x = 0 не входит в область определения, поэтому это лишь меняет границы полуинтервала местами (т. е. если левая граница была исключена, а правая включена, то сейчас наоборот: левая включена, правая исключена). Подставим координаты (0; y) и составим уравнение:
Правая граница исключается, иначе не будет пересечений, левая включается, т. к. при таком a всё ещё будет одно пересечение.
В первом уравнении мы раскрыли модуль: при x > 0 уравнение имеет вид y + a = 1, при x ≤ 0 оно не определено.
График первого уравнения - прямая, параллельная оси Ox, которая определена при x > 0. График второго уравнения - парабола, её вершина имеет координаты (-a; -3). При движении прямой вниз парабола сдвигается влево, а при движении прямой вверх - вправо.
Система имеет одно решение, если прямая касается параболы или парабола пересекает её один раз.
1 случай. Касание. Прямая, которая касается параболы, имеет уравнение y = -3 ⇒ 1 - a = -3 ⇔ a = 4. Но тогда вершина параболы будет иметь координату (-4; -3), а при x < 0 первое уравнение не определено. a = 4 не подходит.
2 случай. Пересечение. Если бы прямая y = 1 - a была определена в точке x = 0, то парабола имела бы одно пересечение с прямой в некой точке (0; y₁), двигалась вправо, пока её левая ветвь вновь не пересекла прямую в точке (0; y₂). Но x = 0 не входит в область определения, поэтому это лишь меняет границы полуинтервала местами (т. е. если левая граница была исключена, а правая включена, то сейчас наоборот: левая включена, правая исключена). Подставим координаты (0; y) и составим уравнение:
Правая граница исключается, иначе не будет пересечений, левая включается, т. к. при таком a всё ещё будет одно пересечение.
ответ: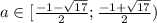
1) Точки экстремума - это точки, в которых производная = 0 или не существует.
Значит, надо искать производную. Сработает формула:
(U/V)' = (U'V - UV')/V²
Начнём.
y'= (-2(x+1) - (3-2x) )/(x+1)² = -5/(х+1)²
Эта производная не равна нулю. Но при х = -1 она не существует.
ответ: х = -1 это точка разрыва.
2)план наших действий:
ищем производную
приравниваем к нулю и решаем уравнение;
Смотрим, какие корни попали в указанный промежуток;
ищем значения функции в этих точках и на концах промежутка;
пишем ответ.
Поехали?
y'= -2/(х² +4)² * 2х= -4х/(х² +4)²
-4х/(х² +4)² = 0, ⇒ х = 0; 0∈[-10;10]
a) x = 0
y = 2/4 = 0,5
x = -10
y = 2/104
х = 10
у = 2/104
ответ: max y = 0,5
min y = 2/104 = 1/52