Пусть треугольник АВС. Высота ВК медиана ВМ. Т.к. углы АВК=углу КВМ , то ВК не только высота , но и биссектриса . Значит треугольник АВМ равнобедренный АВ=ВМ КВ будет и медианой , значит АК=КМ. Но по условию ВМ медиана, значит АМ=МС . Тогда МС=2 КМ. Рассмотрим треугольник КВС. В нём ВМ биссектриса по условию, т.к. по условию три угла равны АВК=КВМ=МВС. Биссектриса внутреннего угла делит противоположну сторону на отрезки, пропорциональные прилежащим сторонам ВК:ВС=КМ:МС= 1:2. Тогда ВС в 2 раза больше ВК. А в прямоугольном треугольнике с острым углом в 30 градусов гипотенуза в 2 раза больше катета, противолежащего этому углу. Тогда угол ВСА=30 градусов. Угол КВС =60 гр. Тогда угол АВС состоит из трёх равных углов и каждый по 30 гр. Угол АВС=90гр. Угол ВАС=60 гр.
S полн. пов =2430
Объяснение:
Sполн. пов=Sбок.пов+2*Sосн
Sбок.пов=Росн*Н, Н - высота призмы
Sосн=S трапеции =(a+b)*h/2, h - высота трапеции
1. ABCD - трапеция
AB=25, BC=16, CD=17, AD=44.
дополнительные построения:
BM_|_AD, CN_|_AD, BC=MN=16
пусть DN=x, тогда
AD=AM+MN+ND
44=AM+16+x,
AM=44-(16+x), AM=28-x
2. рассмотрим прямоугольный треугольник АМВ:
∠M=90°
гипотенуза АВ=25
катет АМ=28-х
катет ВМ найти по теореме Пифагора:
AM²=AB²-BM²
AM²=25²-(28-x)²
AM²=-x²+56x-159
3. рассмотрим прямоугольный треугольник DNC:
гипотенуза CD=17
катет DN=x
катет CN найти по теореме Пифагора:
CN²=CD²-DN²
CN²=17²-x²
4. BM=CN, =>
уравнение: -х²+56x-159=17²-x²
56x=448
x=8
CN²=17²-8², CN=15
5.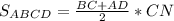
6. S полн. пов=(25+16+17+44)*15+2*450=2430
Биссектриса внутреннего угла делит противоположну сторону на отрезки, пропорциональные прилежащим сторонам ВК:ВС=КМ:МС= 1:2. Тогда ВС в 2 раза больше ВК. А в прямоугольном треугольнике с острым углом в 30 градусов гипотенуза в 2 раза больше катета, противолежащего этому углу. Тогда угол ВСА=30 градусов. Угол КВС =60 гр. Тогда угол АВС состоит из трёх равных углов и каждый по 30 гр. Угол АВС=90гр. Угол ВАС=60 гр.