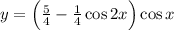Домножаем к левой и правой частям дифференциального уравнения на , имеем . Левую часть уравнения можно представить в виде:
Замечаем, что левая часть последнего диф. уравнения это дифференцирование произведения двух функций и в правой части применяем синус двойного угла.
Осталось найти частное решение, подставив начальные условия
Частное решение данного диф. уравнения:
Домножаем к левой и правой частям дифференциального уравнения на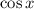 , имеем
, имеем 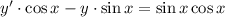 . Левую часть уравнения можно представить в виде:
. Левую часть уравнения можно представить в виде:
Замечаем, что левая часть последнего диф. уравнения это дифференцирование произведения двух функций и в правой части применяем синус двойного угла.
Осталось найти частное решение, подставив начальные условия
Частное решение данного диф. уравнения: