Её можно получить из графика гиперболы путём сдвига на 2 единицы влево вдоль оси ОХ.
Асимптота заданной гиперболы - прямая х= -2 .
Точки, через которые проходит график: (0,3) , (4,1) , (-4,-3) , (1,2) , (-1,6) , (-4,-3) .
На отрезке [0,4] наибольшее значение при х=0, а наименьшее - при х=4, так как на этом отрезке функция убывает и бОльшему значению аргумента (4>0) соответствует мЕньшее значение функции: y(4)<y(0).
Графиком функции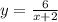
является гипербола.
Её можно получить из графика гиперболы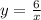
путём сдвига на 2 единицы влево вдоль оси ОХ.
Асимптота заданной гиперболы - прямая х= -2 .
Точки, через которые проходит график: (0,3) , (4,1) , (-4,-3) , (1,2) , (-1,6) , (-4,-3) .
На отрезке [0,4] наибольшее значение при х=0, а наименьшее - при х=4, так как на этом отрезке функция убывает и бОльшему значению аргумента (4>0) соответствует мЕньшее значение функции: y(4)<y(0).
у(наибол)=у(0)=3 , у(наимен)=у(4)=1
На области определения функция убывающая.
площадь прамоугольника S = a * b;
пусть меньшая сторона = х, тогда большая = х+5
составим уравнение
x * (x + 5) = 50
x² + 5x = 50
x²+5x - 50 = 0
по теореме виета
х1*х2=-50
х1+х2=-5
х1=-10; х2=5;
так как длина стороны не может иметь отрицательное значение нам подойдет только х2, следовательно
1. ширина площадки: 5 м
длина: 5 + 5 = 10 м
бордюр будет укладываться по периметру площадки
P = (5 + 10 ) * 2 = 30 м
так как 30/8=3,75 нашим горе строителям придется купить 4 упаковки и оставить 2 метра бордюра себе