Разложи на множители: (y6+x6)2−(y6−x6)2−y2x2. (Может быть несколько вариантов ответа! Выбери все возможные варианты, которые могут получиться.)

x2(4y6x4+2x10−y2x)
4y6x6+2x12−y2x2
(2y3x3−yx)⋅(2y3x3+yx)
Другой ответ
x2(2x4−y2x)
y2x2⋅(4y4x4−1)
y2x2⋅(2y2x2−1)⋅(2y2x2+1)

Показать ответ

Ответ:

lavbi3

27.03.2023 05:56

(см. объяснение)

Объяснение:

(1+a^2)x^6+3a^2x^4+2(1-6a)x^3+3a^2x^2+a^2+1=0

Заметим, что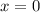 x=0 не является корнем уравнения.

Тогда поделим его на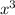 x^3 :

$(1+a^2)x^3+3a^2x+2(1-6a)+\dfrac{3a^2}{x}+\dfrac{a^2+1}{x^3}=0$

Выполним группировку:

$(1+a^2)\left(x^3+\dfrac{1}{x^3}\right)+3a^2\left(x+\dfrac{1}{x}\right)+2(1-6a)=0$

Заметим, что если - корень уравнения, то $\dfrac{1}{x}$ тоже.

Тогда единственное решение возможно, если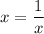 $x=\dfrac{1}{x}$ .

Иными словами, исходное уравнение может иметь ровно один корень тогда, когда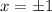 $x=\pm1$ .

Подставляя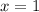 x=1 в исходное уравнение, получаем, что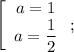 $\left[\begin{array}{c}a=1\\a=\dfrac{1}{2}\end{array}\right;$

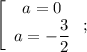
Подставляя x=-1 , получаем, что $\left[\begin{array}{c}a=0\\a=-\dfrac{3}{2}\end{array}\right;$

Теперь решим уравнение при каждом найденном значении параметра и отберем те, при которых имеется единственное решение.

Выполнив необходимые вычисления, получаем, что каждое значение параметра подходит.

Итого при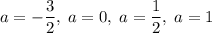 $a=-\dfrac{3}{2},\;a=0,\;a=\dfrac{1}{2},\;a=1$ исходное уравнение имеет единственное решение.

Задание выполнено!

0,0(0 оценок)

Ответ:

revazhora

18.01.2022 23:24

$\alpha=0.5$ - вероятность победы

Иван и Алексей сыграют друг с другом в 1 туре, если так будет определено жеребьевкой.

Рассмотрим возможных соперников Ивана. Их 15 человек. Поэтому, вероятность того, что по результатам жеребьевки 1 тура Иван будет играть именно с Алексеем равна:

$g_1=\dfrac{1}{15}$

Таким образом, вероятность сыграть Ивану и Алексею в 1 туре между собой равна:

$p_1=g_1=\dfrac{1}{15}$

Если Иван и Алексей не сыграли между собой в 1 туре, то возможно они сыграют между собой во 2 туре. Но для этого каждому из них необходимо как минимум выиграть в 1 туре.

Вероятность того, что и Иван и Алексей окажутся во 2 туре, равна:

$p_2'=\left(1-p_1\right)\cdot\alpha \cdot\alpha =\left(1-\dfrac{1}{15}\right)\cdot0.5\cdot0.5=\dfrac{14}{15}\cdot\dfrac{1}{2}\cdot\dfrac{1}{2}=\dfrac{7}{30}$

Во 2 туре играет 8 человек, то есть 7 возможных соперников для каждого. По результатам жеребьевки 2 тура Иван будет играть с Алексеем с вероятностью:

$g_2=\dfrac{1}{7}$

Значит, играть Иван и Алексей между собой во 2 туре будут с вероятностью:

$p_2=p_2'\cdot g_2=\dfrac{7}{30} \cdot\dfrac{1}{7} =\dfrac{1}{30}$

Если Иван и Алексей не играли между собой во 2 туре, то они имеют шансы выйти в 3 тур. Это произойдет с вероятностью:

$p_3'=p_2'\cdot(1-g_2)\cdot\alpha\cdot\alpha= \dfrac{7}{30}\cdot \left(1-\dfrac{1}{7}\right)\cdot0.5\cdot0.5=\dfrac{7}{30}\cdot\dfrac{6}{7}\cdot\dfrac{1}{2}\cdot\dfrac{1}{2}=\dfrac{1}{20}$

В 3 туре играет 4 человека, то есть 3 возможных соперника для каждого. По результатам жеребьевки 2 тура Иван будет играть с Алексеем с вероятностью:

$g_3=\dfrac{1}{3}$

Значит, Иван и Алексей сыграют между собой в 3 туре с вероятностью:

$p_3=p_3'\cdot g_3=\dfrac{1}{20} \cdot\dfrac{1}{3} =\dfrac{1}{60}$

Вероятность выхода Ивана и Алексея в 4 тур:

$p_4'=p_3'\cdot(1-g_3)\cdot\alpha\cdot\alpha=\dfrac{1}{20}\cdot \left(1-\dfrac{1}{3}\right)\cdot0.5\cdot0.5=\dfrac{1}{20}\cdot\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot\dfrac{1}{2}=\dfrac{1}{120}$