Реши графически систему уравнений:
{y=2x+1
{y=−2x−3

ответ (записать координаты точки пересечения или слово «нет»):
{x=
y=

ответ: 21,6 км/ч.

Объяснение: Пусть х км/ч собственная скорость лодки (скорость лодки в стоячей воде), у км/ч скорость течения реки. Время которое затратила лодка по течению реки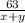 часов, а против течения реки 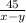часов и на весь путь затрачено 5 часов. Расстояние которое лодка проходит  за 5 часов по течению будет 5(х+у) км, а такое же расстояние против течения за 7 часов будет 7(х-у) км. Составим два уравнения:

5(х+у)=7(х-у)

Выделим скорость течения реки (у) во втором  уравнении:

5(х+у)=7(х-у); ⇒ 5х+5у=7х-7у; ⇒ 12у=2х; ⇒ у=x/6.

Полученное значение подставим в первое уравнение:

x=21,6 (км/ч) собственная скорость катера.

1)  замена   ху=  u   x-y=v

u  + 2v=10   домножим на 5 и отнимем эти 2 уравнения     13v=39.   v=3, подст в 1 ур  

5u-3v=11                                                                                       u +6=10    u=4

вернемся к замене   ху=4      х-у=3,    х=у+3,     (у+3)*у=4

у квадрат +3у -4 =0   у1=-4,  у2=1

                                х1=-1,  х2=4

(-1;-4)   (4;1)

2) в 1 ур  формула  (х-у)(х+у)=-32  подст из 2 ур  получаем  (х-у)*16=-32,  х-у=-2

имеем простую систему  х+у =16, х-у=-2  сложим их и отнимем др от др

2х=14  х=7,    2у=18  у=9

(7;9)