Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
А
Английский язык
Х
Химия
Э
Экономика
П
Право
И
Информатика
У
Українська мова
Қ
Қазақ тiлi
О
ОБЖ
Н
Немецкий язык
Б
Беларуская мова
У
Українська література
М
Музыка
П
Психология
А
Алгебра
Л
Литература
Б
Биология
М
МХК
О
Окружающий мир
О
Обществознание
И
История
Г
Геометрия
Ф
Французский язык
Ф
Физика
Д
Другие предметы
Р
Русский язык
Г
География
Показать больше
Показать меньше
eegorov1996
21.09.2021 00:55 •
Алгебра
Решить уравнение a)3^1-2x=45x (3 в степени 1-2x равно 45x) б) 2^x+1=5^1-3x (2 в степени x+1 равно 5 в степени 1-3x)
Показать ответ
Ответ:
marimitul
17.08.2020 08:54
a
Введём W-функцию Ламберта. Её свойство:
.
Тогда,
б
0,0
(0 оценок)
Популярные вопросы: Алгебра
cygrobik111
01.02.2023 23:08
Решить уравнение относительно параметра а: | х + 3 | - 2 = а. построить график у = | х - 3 | + | х + 3 |...
мединалуна
25.06.2021 05:26
Кожну сторону квадра збільшити на 2, 5 см, у результаті чого його площа збільшилася на 131,25см^2. знайди сторону більшого квадрата...
kornev183
24.02.2021 12:42
Укажите вектор ортогональный вектору (1-2,5):...
Нуртилек2664467
21.12.2022 07:57
Найдите область определения функции f(x)=корень из 15-2x-x^2(конец корня) + 1/x^2-9...
Ddf001
19.04.2020 04:23
Сколько целых чисел расположено между числами v17 - 1 и v37 где v17 там только 17 под корнем...
Кпоперша1
10.04.2020 20:34
Разложите на множители квадратный трехчлен: x^2-11x+24...
juehxbrf
10.04.2020 20:34
Из четырех тузов случайным образом поочередно вытащили две карты.найдите вероятность того чтообе карты -тузы черной масти...
ruslan2003185
18.06.2022 00:05
При каких натуральных n и k многочлен x^n-1 делится без остатка на многочлен x^k-1?...
Minimuux
28.10.2022 02:52
3. катер в 10: 00 вышел из пункта а в пункт в, расположенный в 15 км от а. пробыв в пункте в 1 час 15 минут, катер отправился назад и вернулся в пункт а в 14: 00 того...
Keyanplay1
14.01.2022 11:27
Сторона первого квадрата на 2 см больше стороны второго квадрата а площадь первого квадрата на 48 см в квадрате больше площади второго найдите стороны квадратов...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
a
Введём W-функцию Ламберта. Её свойство: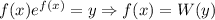 .
.
Тогда,
б