так как для любого действительного х:
то
поэтому
причем равенство достигается только тогда когда
а
откуда из первого sin x=1 V sin x=-1 V sin x=0
со второго cos x=1 или cos x=0
учитывая, что когда sin x=1 V sin x=-1 то cos x=0 (по основному тригонометрическому тождеству) а когда cos x=1 то sin x=0, по модулю одновременно они не могут быть равными 1, то
решениями будут
ответ: n є Z ; k є Z
так как для любого действительного х: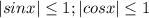
то
поэтому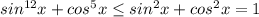
причем равенство достигается только тогда когда
откуда из первого sin x=1 V sin x=-1 V sin x=0
со второго cos x=1 или cos x=0
учитывая, что когда sin x=1 V sin x=-1 то cos x=0 (по основному тригонометрическому тождеству) а когда cos x=1 то sin x=0, по модулю одновременно они не могут быть равными 1, то
решениями будут
ответ: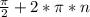 n є Z
n є Z 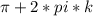 ; k є Z
; k є Z