Решите задачу (переформулируйте условие так, чтобы было легче составить уравнение):
От станции к озеру вышел пешеход со скоростью 4 км/ч.Через 0,5 вслед за ним по той же станции и по такой же дороге отправился велосипедист со скоростью 12 км/ч.К озеро они прибыли одновременно.Определите, сколько времени шёл пешеход и чему равно расстояние от станции до озера.
1) f(x) =x⁴ + 4·sin²x·cos²x - чётная функция
2) f(x) =x⁴ + 4·sin²x·cos²x - нечётная функция
Объяснение:
Определение. Функция f(x), x∈X, называется чётной, если для любого значения x из множества X выполняется равенство: f(–x) = f(x).
Определение. Функция f(x), x∈X, называется нечётной, если для любого значения x из множества X выполняется равенство: f(–x) =–f(x).
Известно, что функция:
sinx – нечётная, cosx - чётная, tgx – нечётная, ctgx – нечётная.
Решение.
1) Функция f(x) =x⁴ + 4·sin²x·cos²x определена при всех x∈R. Проверим по определению при x∈R:
f(–x) = (–x)⁴ +4·sin²(–x)·cos²(–x) = x⁴ +4·(–sinx)²·cos²x =
= x⁴ +4·sin²x·cos²x = f(x), то есть f(–x) = f(x) и функция – чётная;
2) Функция f(x) = (tgx – ctgx)/cosx определена при всех x∈X=R\{πn, π/2+πk, n∈Z, k∈Z}. Проверим по определению при x∈X:
f(–x) = (tg(–x) – ctg(–x))/cos(–x) = (–tgx –(–ctgx))/cosx =
= –(tgx – ctgx)/cosx = –f(x), то есть f(–x) = –f(x) и функция – нечётная.
Объяснение:
Пусть длина участка равна х м., а ширина - у м. Зная, что периметр = 160 м, а формула для нахождения периметра P=2*(a+b) и площадь участка = 1596 м^2 а формула S=a*b, составим систему уравнений:
Выразив одну величину через другую, выполним подстановку и решим уравнение с одним неизвестным, получим :
(80-у)*у=1596
80у-у^2=1596
y^2-80y+1596=0
D=b^2-4ac=80^2-4*1*1596=6400-6384=16 D>0, уравнение имеет 2 корня:
у1,2=(-b±√D)/2a
y1=(80-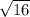
)/2*1=(80-4)/2=76/2=38
y2=(80+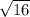
)/2*1=(80+4)/2=84/2=42
Тогда х1+38=80
х1=80-38=42
х2+42=80
х2=80-42=38. Значит размеры садового участка равны 38 м и 42 м, меньший из них равен 38 м