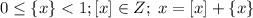смешали 4 литра 35-процентного раствора вещества с 11 литрами 5-процентного раствора этого же вещества. сколько процентов составляет концентрация раствора
Решим неравенство методом интервалов: Нули функции будут в точках: 4; 1,5; 2/3 (просто приравнять уравнения в скобках к нулю) Отмечаем нули функции на координатной прямой в порядке их возрастания. Все точки выколоты, т.к. неравенство строгое. Для того чтобы узнать как расположить знаки под интервалами выбираем произвольное число кроме тех, которые являются нулями функции. Возьмем, например, 0. Если х = 0, то 3*0-2= -2 (знак отрицательный) 0-4= -4 (знак отрицательный) 3-2*0 = 3 (знак положительный) Перемножаем все числа (-2)(-4)*3 = 24 (знак положительный) => под интервалом будет "+". Нуль находится в пределах от минус бесконечности до 2/3. Ставим там "+". Далее знаки чередуются. Теперь нам нужен ответ. Т.к. у нас < следовательно нам нужно все что меньше нуля, тобишь под знаком "-". Выписываем интервалы и получаем конечный ответ.
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение
2)
А значит, если взять (*), . И правда:
(*) Очевидно, что для любого допустимого значения выражение определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4)
А значит, если взять (**), . И правда:
(**) Очевидно, что для любого допустимого значения выражение определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда
4)
___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x.
Нули функции будут в точках: 4; 1,5; 2/3 (просто приравнять уравнения в скобках к нулю)
Отмечаем нули функции на координатной прямой в порядке их возрастания. Все точки выколоты, т.к. неравенство строгое. Для того чтобы узнать как расположить знаки под интервалами выбираем произвольное число кроме тех, которые являются нулями функции.
Возьмем, например, 0.
Если х = 0, то
3*0-2= -2 (знак отрицательный)
0-4= -4 (знак отрицательный)
3-2*0 = 3 (знак положительный)
Перемножаем все числа (-2)(-4)*3 = 24 (знак положительный) => под интервалом будет "+".
Нуль находится в пределах от минус бесконечности до 2/3. Ставим там "+". Далее знаки чередуются.
Теперь нам нужен ответ. Т.к. у нас < следовательно нам нужно все что меньше нуля, тобишь под знаком "-". Выписываем интервалы и получаем конечный ответ.
По определению,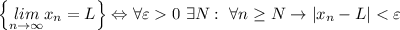
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение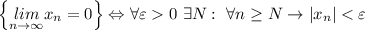
2)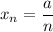
А значит, если взять![N=\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/0d89e.png) (*),
(*), 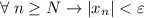 . И правда:
. И правда: 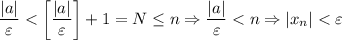
(*) Очевидно, что для любого допустимого значения выражение
выражение ![\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/ae843.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4)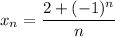
А значит, если взять![N=\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/a4ca4.png) (**),
(**), 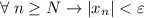 . И правда:
. И правда: ![\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|](/tpl/images/3820/0626/49458.png)
(**) Очевидно, что для любого допустимого значения выражение
выражение ![\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/698f8.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда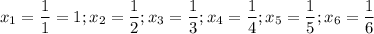
4)
___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x.