а - длина прямоугольника b - ширина прямоугольника ================================================================= Р=22 см S=30 см² а - ? см b - ? см Решение: (1)
(2)
из формулы площади прямоугольника (2) выводим формулу нахождения ширины
подставляем в формулу периметра прямоугольника (1)
/·a
умножаем на а для того, чтобы избавиться от знаменателя
подставим в уравнение данные P и S
Квадратное уравнение имеет вид:
Считаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
Следовательно, стороны равны 6см и 5см соответственно
ответ: 6см и 5см стороны прямоугольника. Проверка: Р=2(а+b)=2(6+5)=2·11=22 (см) S=a·b=6·5=30 (м²)
квадрат длины гипотенузы равен сумме квадратов длин катетов. отсюда,
==
длина гипотенузы 50см.
при вращении прямоугольного треугольника вокруг гепотенузы, он описывает окружность. значит, нам надо найти площадь описанной окружности.
как мы знаем, центр окружности, описанной вокруг прямоугольного треугольника, совпадает с серединой гипотенузы, а радиус R такой окружности равен половине гипотенузы. значит, R=h/2=50/2=25см.
далее находим площадь S круга по формуле S=пи*R^2=3,14*25^2=3.14*625=1962.5
а - длина прямоугольника
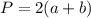 (1)
(1)
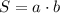 (2)
(2)
b - ширина прямоугольника
=================================================================
Р=22 см
S=30 см²
а - ? см
b - ? см
Решение:
из формулы площади прямоугольника (2) выводим формулу нахождения ширины
подставляем в формулу периметра прямоугольника (1)
умножаем на а для того, чтобы избавиться от знаменателя
подставим в уравнение данные P и S
Квадратное уравнение имеет вид:
Считаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
Следовательно, стороны равны 6см и 5см соответственно
ответ: 6см и 5см стороны прямоугольника.
Проверка:
Р=2(а+b)=2(6+5)=2·11=22 (см)
S=a·b=6·5=30 (м²)
с теоремы Пифагора находим длину гипотенузы.
квадрат длины гипотенузы равен сумме квадратов длин катетов. отсюда,
длина гипотенузы 50см.
при вращении прямоугольного треугольника вокруг гепотенузы, он описывает окружность. значит, нам надо найти площадь описанной окружности.
как мы знаем, центр окружности, описанной вокруг прямоугольного треугольника, совпадает с серединой гипотенузы, а радиус R такой окружности равен половине гипотенузы. значит, R=h/2=50/2=25см.
далее находим площадь S круга по формуле S=пи*R^2=3,14*25^2=3.14*625=1962.5