В лотерее на 20000 билетов приходится 943 призовых. Чему равна вероятность, что купленный билет окажется без выигрыша?

Показать ответ

Ответ:

Sofa1351

10.08.2020 08:20

Для решения запишем формулу бинома Ньютона:

$(a+b)^n=a^n+C_n^1a^{n-1}b+C_n^2a^{n-2}b^2+...+b^n$

Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение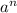 a^n .

Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение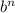 b^n .

Рассмотрим многочлен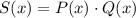 $S(x)=P(x)\cdot Q(x)$ , где:

$P(x)=(3x^7+6x^4-1)^{12}$

Q(x)=(5x^2+2)^3

Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.

Для многочлена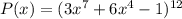 $P(x)=(3x^7+6x^4-1)^{12}$ :

- степень определяется выражением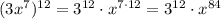 $(3x^7)^{12}=3^{12}\cdot x^{7\cdot12}=3^{12}\cdot x^{84}$ , то есть степень равна 84

- свободный член равен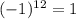 $(-1)^{12}=1$

Для многочлена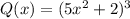 Q(x)=(5x^2+2)^3 :

- степень определяется выражением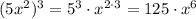 $(5x^2)^3=5^3\cdot x^{2\cdot3}=125\cdot x^6$ , то есть степень равна 6

- свободный член равен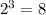 2^3=8

Наконец, для многочлена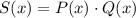 $S(x)=P(x)\cdot Q(x)$ получим:

- степень определяется выражением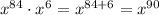 $x^{84}\cdot x^6=x^{84+6}=x^{90}$ , то есть степень равна 90

- свободный член равен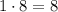 $1\cdot8=8$

Сумма степени и свободного члена многочлена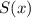 S(x) :

90+8=98

ответ: 98

0,0(0 оценок)

Ответ:

Yuki16

08.01.2022 01:53

Интересная задачка.

Для того, чтобы начать решать эту задачу, нам необходимо найти такую последовательность, которая приносила бы нам всегда удачу! Из условия ясно, что начинающий должен ходить первый. Можно предложить такой вариант ходов:
Начинающий должен взять один карандаш. Остается 17 штук. Какое бы количество карандашей ни взял противник, обязательно нужно оставить 13 карандашей на столе. По такому же раскладу, надо оставить 9 карандашей, а затем 5. Какое бы количество карандашей не взял соперник, начинающий всегда сможет оставить ему 1 карандаш.

0,0(0 оценок)

Популярные вопросы: Алгебра