Пассажирский поезд был задержан в пути на 16 минут и нагнал опоздание на перегоне в 80км, идя со скоростью на 10км/ч больше, чем полагалось по расписанию. Какова была скорость поезда по расписанию? ​

Все неравенства сравнивают с нулем.

Поэтому переносим 1 влево

и приводим к общему знаменателю:

Дробь отрицательна, когда числитель и знаменатель имеют разные знаки:

    или  

    или  

Умножаем первое неравенство каждой системы на (-1)

и меняем знак неравенства:

    или  

Выбираем пересечение множеств, заданных каждым неравенством системы:

   или    

О т в е т. (-∞; 0) U (1; +∞)

Умножаем числитель на (-1) и меняем знак

Решаем методом интервалов:

находим нули числителя:

х=1

и нули знаменателя:

х=0

Эти две точки разбивают числовую прямую на три промежутка. Находим знак дроби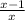  на каждом промежутке и

расставляем знаки:

__+___ (0) __-__ (1) __+__

О т в е т. (-∞; 0) U (1; +∞)

(4; 2)

Найти координаты точки пересечения

прямых.

Объяснение:

1.

Построить график функции

у=2х-3

Уравнение линейной функции:

у=kx+b

k=2; b=-3

График не является прямой пропорци

ональностью ( так как не проходит через

точку начала отсчета)

k>0 ==> линейная функция возрастает

b=-3 относительно нулевой точки на оси

ординат график опущен вниз на 3ед.

Пересечение с ОУ:

у=0

0=2х-3

-2х=-3

х=(-3)/(-2)

х=1,5

(1,5; 0)

Пересечение с ОХ:

х=0

у=2×0-3

у=0-3

у=-3

(0; -3)

Для построения графика построим и за

полним таблицу ( достаточно двух точек):

Х 0 4

У -3 5

2.

Чтобы найти координаты точек пересече

ния двух прямых, решаем систему

двух уравнений:

{2х-у=6 | ×(-2)

{х+2у=8

{4х-2у=12

{х+2у=8

Складываем оба уравнения:

{4х+х=20

{х+2у=8

{5х=20

{2у=8-х

{х=20:5

{у=(8-х)/2

{х=4

{у=(8-4)/2

{х=4

{у=2

ответ: (4; 2)