1) Поскольку грузовики обладают одинаковой грузоподъемностью, то максимально возможное перевозимое количество товара прямо пропорционально числу грузовиков (если речь идет о фиксированном числе рейсов).
2) Если количество продуктов не меняется, то при равномерном их распределении на каждый из дней похода длительность похода обратно пропорциональна норме продуктов на один день (чем больше число дней похода, тем меньше норма продуктов на один день).
3) Площадь трапеции равна полусумме оснований умноженной на высоту трапеции, поэтому связь между длиной стороны и площадью трапеции не являются ни прямой, ни обратной пропорциональностью.
и множество натуральных чисел ℕ. Замечу, что при любом k дробь вида является несократимой, то есть если выписывать такие дроби, начиная с k = 1 и увеличивая каждый раз переменную k на 1, ни одна из них не повторится (так как знаменатель постоянно увеличивается).
Покажем, что между этими двумя множествами можно установить взаимно однозначное соответствие. Для этого всем дробям вида , где , поставим в соответствие число . С одной стороны, согласно построению каждой такой дроби будет соответствовать натуральное , притом единственное. С другой стороны, для каждого натурального можно указать единственную (смотри замечание в предыдущем абзаце) дробь вида , и все они будут принадлежать множеству A, поскольку пробегает все натуральные значения. Итак, построенное соответствие действительно взаимно однозначное. А раз множество ℕ счетное, то и множество A также счетное.
1) Поскольку грузовики обладают одинаковой грузоподъемностью, то максимально возможное перевозимое количество товара прямо пропорционально числу грузовиков (если речь идет о фиксированном числе рейсов).
2) Если количество продуктов не меняется, то при равномерном их распределении на каждый из дней похода длительность похода обратно пропорциональна норме продуктов на один день (чем больше число дней похода, тем меньше норма продуктов на один день).
3) Площадь трапеции равна полусумме оснований умноженной на высоту трапеции, поэтому связь между длиной стороны и площадью трапеции не являются ни прямой, ни обратной пропорциональностью.
Рассмотрим множество A, заданное в условии:
и множество натуральных чисел ℕ. Замечу, что при любом k дробь вида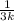
является несократимой, то есть если выписывать такие дроби, начиная с k = 1 и увеличивая каждый раз переменную k на 1, ни одна из них не повторится (так как знаменатель постоянно увеличивается).
Покажем, что между этими двумя множествами можно установить взаимно однозначное соответствие. Для этого всем дробям вида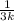
, где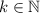 
, поставим в соответствие число 
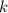. С одной стороны, согласно построению каждой такой дроби будет соответствовать натуральное 
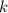, притом единственное. С другой стороны, для каждого натурального 
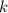можно указать единственную (смотри замечание в предыдущем абзаце) дробь вида 
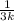, и все они будут принадлежать множеству A, поскольку 
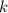пробегает все натуральные значения. Итак, построенное соответствие действительно взаимно однозначное. А раз множество ℕ счетное, то и множество A также счетное.