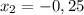В партии однотипных деталей стандартные составляют 96%. Наугад из партии берут 500 деталей. Определите среднее квадратическое отклонение (Х) для дискретной случайной величины Х — появления числа стандартных деталей среди 500 наугад взятых. ответ запишите в виде десятичной дроби, округлив до тысячных
1-ый токарь 2-ой токарь 3-ий токарь
Производит-ть, дет./ч. 6 5 х
Время работы до того,
как 3-ий догонит 2-го, ч. у+2 у+1 у
К-во изготовл. деталей
за то время пока 3-ий
догоняет 2-го 6(у+2) 5(у+1) ху или 5(у+1)
Время работы до того,
как 3-ий догонит 1-го, ч. у+2+2=у+4 у+1+2=у+3 у+2
К-во изготовл. деталей
за то время пока 3-ий
догоняет 1-го 6(у+4) 5(у+3) х(у+2) или 6(у+4)
Составим и решим систему уравнений:
ху=5(у+1)
х(у+2)=6(у+4)
х=5(у+1)/у
(у+2)*5(у+1)/у=6(у+4)
х=5(у+1)/у
5(у+2)(у+1)=6у(у+4)
х=5(у+1)/у
5у^2+10у+5y+10=6у^2+24у
х=5(у+1)/у
6у^2+24у-5у^2-15y-10=0
х=5(у+1)/у
у^2+9у-10=0
х=5(у+1)/у
по теореме Виета:
у1=1 у2=-10 (не подходит, так как время не может быть отрицательным)
х=5(1+1)/1
у=1
х=10
у=1
ответ: производительность труда третьего токаря - 10 деталей в час.
Для того чтобы найти корни необходимо данные выражения приравнять к нулю
1)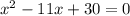
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
ответ: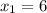 ;
; 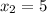
=================================================================
2)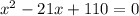
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
ответ: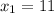 ;
; 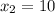
==================================================================
3)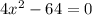
ответ: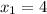 ;
; 
=================================================================
4)
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
ответ: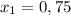 ;
;