Случайная величина Х - количество попаданий в кольцо. Случайная величина распределена по биномиальному закону. Вероятность успеха в одном испытании p = 0.1, тогда q = 1 - p = 0.9
1) Вероятность того, что баскетболист не попадает в кольцо ниразу
2) Вероятность того, что баскетболист попадет один раз
3) Вероятность того, что баскетболист попадет два раза
4) Вероятность того, что баскетболист попадет три раза
Закон распределения случайной величины X:
Xi 0 1 2 3
Pi 0.729 0.243 0.027 0.001
Математическое ожидание случайной величины X:
Иначе мат. ожидание можно подсчитать, если Х - распределена по биномиальному закону то
Случайная величина Х - количество попаданий в кольцо. Случайная величина распределена по биномиальному закону. Вероятность успеха в одном испытании p = 0.1, тогда q = 1 - p = 0.9
1) Вероятность того, что баскетболист не попадает в кольцо ниразу
2) Вероятность того, что баскетболист попадет один раз
3) Вероятность того, что баскетболист попадет два раза
4) Вероятность того, что баскетболист попадет три раза
Закон распределения случайной величины X:
Xi 0 1 2 3
Pi 0.729 0.243 0.027 0.001
Математическое ожидание случайной величины X:
Иначе мат. ожидание можно подсчитать, если Х - распределена по биномиальному закону то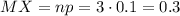
Дисперсия случайной величины X:
Иначе: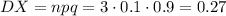
Среднее квадратическое отклонение:
Объяснение:
У нас есть V (скорость), t (время) и S (расстояние)
Лодка двигалась ПО течению реки. Ее собственная скорость остаётся неизвестна. Соответственно:
1) х км/ч + 4км/ч = это общая скорость с которой двигалась лодка.
Далее у нас даётся время за которое лодка расстояние.
2) Время: за 6 часов.
3) Расстояние: 102 километра.
Мы записываем таблицу
V T S
x+4. 6. 102
И тут мы видим что нам дано все из данных. Это уравнение:
(х+4) × 6 = 102
6х+24=102
6х=78 |: 6
х=13 км/ч скорость лодки.
Проверяем: (13+4)×6=102