Выберите систему уравнений, решением которой является пара чисел (-1; 2) (все системы) 1) 1/x -1 =2y x2 + y2 = 5 2) x2 + y = 3 x + y/2 =1 3) 3y - 2x = 7 -2/x =y 4) 2x + 3y = y x2 -3 = y

Показать ответ

Ответ:

ксю882

08.10.2021 14:50

Объяснение:

24.121

я, конечно прощения, но члены арифметической прогрессии обозначаются как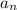 $\displaystyle a_n$ (у вас это 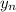$\displaystyle y_n$ ) а разность арифметической прогрессии обозначается как b (у вас это d) я буду обзначать так, как принято в математике

а₁₀ = -19

d= -2

применим формулу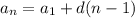 $\displaystyle a_n=a_1+d(n-1)$

a₁₀ = a₁ + (-2)*9 = -19 a₁ = -19 +18 = -1

применим ту же формулу

a₅ = a₁ +4d = 13 ⇒ a₁ = 13-4d

a₁₆ = a₁ + 15d = 46 подставим сюда a₁ = 13-4d получим

13-4d +15d = 46 ⇒ 11d = 33 ⇒ d = 3

тогда

a₁ = 13-4d = 13 - 12 = 1

24.123

всё та же формула

$\displaystyle a_n=a_1+d(n-1) = 24$

8 +3(n-1) = 24

8+3n -3 = 24

3n = 24-5 = 17 здесь нет целого решения для n ⇒ 24 не есть член арифметической прогрессии

0,0(0 оценок)

Ответ:

ClarisVerbis

16.03.2022 02:48

ответ: -3, -2, -1.

Объяснение: Первое условие говорит, что числа должны быть строго меньше нуля (то есть без самого нуля), а второе — что наши числа строго больше -4 (что значит без числа -4) и строго меньше нуля (без нуля).

Эти два условия должны быть соблюдены для выполнения задания.

3 > 0, что неверно

2 > 0, что неверно

-4 < -3 < 0, утверждение верно

-4 <= -4, что неверно

-4 < -2 < 0, утверждение верно

5 > 0, что, неверно

-5 < -4, что неверно

4 > 0, что неверно

-4 < -1 < 0, утверждение верно

1 > 0, что неверно

0 = 0, что неверно