Запишем данные в таблицу, по строке выразим время движения каждого велосипедиста (расстояние разделить на скорость).
Время движения первого велосипедиста:
ч
Время движения второго велосипедиста:
ч
Известно, что первый велосипедист прибывает к финишу на 2 ч раньше второго, т.е. время движения у него меньше. Вычитаем из большего времени меньшее и получаем уравнение:
x > 0 по смыслу задачи, поэтому умножаем на знаменатель обе части уравнения.
6 км/ч
Объяснение:
Пусть х км/ч - скорость второго велосипедиста,
(х + 4) км/ч - скорость первого.
Оба велосипедиста проехали по 30 км.
Запишем данные в таблицу, по строке выразим время движения каждого велосипедиста (расстояние разделить на скорость).
Время движения первого велосипедиста:
Время движения второго велосипедиста:
Известно, что первый велосипедист прибывает к финишу на 2 ч раньше второго, т.е. время движения у него меньше. Вычитаем из большего времени меньшее и получаем уравнение:
x > 0 по смыслу задачи, поэтому умножаем на знаменатель обе части уравнения.
По теореме, обратной теореме Виета,
104.
a) cos 120 =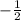
б) sin(-150)= -sin 150=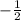
в) tg(-225)= -tg 225 = -1
г) cos(-225)=cos 225=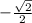
д) cos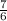
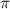= cos 630 = 0
е)sin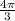
= sin 240 =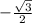
106.
а) sin (
-
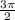) = sin (
-270) = sin (270-
) = -cos 
б) cos (
-
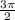)= cos (
-270) = cos (270-
) = -sin 
в) tg (
-2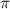
) = tg (
-360) = tg (360-
) = -tg 
Объяснение:
104.
cos(-α)= cos α
sin(-α)= -sin α
tg(-α)= -tg α
ctg(-α)= -ctg α
a) cos 120 =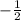
б) sin(-150)= -sin 150=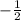
( т.к. sin непарная функция => sin(-α)= -sin α )
в) tg(-225)= -tg 225 = -1 ( т.к. tg непарная функция => tg(-α)= -tg α )
г) cos(-225)=cos 225=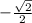
( т.к. cos парная функция => cos(-α)= cos α )
д) cos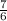
= 
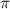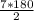=630, 630=360+270 ( 360 это один полный оборот)
=> cos 270 cos 270 = 0
е)sin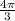
= sin 240 =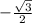
106.
В этом номере я использовал формулы приведения
их можно найти в интернете
а) sin (
-
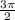) = sin (
-270) = sin (270-
) = -cos 
б) cos (
-
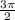)= cos (
-270) = cos (270-
) = -sin 
в) tg (
-2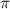
) = tg (
-360) = tg (360-
) = -tg 