Трёхзначное число содержит три цифры, по условию только одна из которых 3.
1) Числа вида . Цифры a и b могут быть любыми из оставшихся девяти цифр. Всего трёхзначных чисел с единственной тройкой в разряде сотен 9·9=81.
2) Числа вида и . Цифры c и m могут быть любыми из восьми (1,2,4,5,6,7,8,9), а цифры d и n могут быть любыми из девяти (0,1,2,4,5,6,7,8,9). Всего трёхзначных чисел с единственной тройкой в разряде десяток 8·9=72. И столько же с единственной тройкой в разряде единиц 8·9=72.
Берешь это в табличку : y| 1 | 3 | x| 2 | 3 | Если y = 1, то x = 2; если y = 3, то x = 3. Делала так: Подбирала любое значение y и находила значение x, как в любом уравнении. На примере первого : 1=2x-3; x=2. Во втором так же. Далее на координатной плоскости отмечаем точки с координаты и, полученными ранее. Например точка K ( 2;1) и точка L (3;3). Обратите внимание, что в ответе координаты точки А мы пишем именно в таком порядке, т.к. На первом месте значение х, а на втором у. Когда вы отметили точки, вы вполне можете провести через них прямую, сделайте это. И лучше провести ее через всю плоскость, а не от точки до точки. Удачи!
Всего 10 цифр : 0,1,2,3,4,5,6,7,8,9
Трёхзначное число содержит три цифры, по условию только одна из которых 3.
1) Числа вида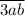
. Цифры a и b могут быть любыми из оставшихся девяти цифр. Всего трёхзначных чисел с единственной тройкой в разряде сотен 9·9=81.
2) Числа вида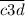
и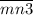 
. Цифры c и m могут быть любыми из восьми (1,2,4,5,6,7,8,9), а цифры d и n могут быть любыми из девяти (0,1,2,4,5,6,7,8,9). Всего трёхзначных чисел с единственной тройкой в разряде десяток 8·9=72. И столько же с единственной тройкой в разряде единиц 8·9=72.
Тогда всего трёхзначных чисел с одной тройкой
81 + 72 + 72 = 225
ответ : 225
Берешь это в табличку : y| 1 | 3 | x| 2 | 3 | Если y = 1, то x = 2; если y = 3, то x = 3. Делала так: Подбирала любое значение y и находила значение x, как в любом уравнении. На примере первого : 1=2x-3; x=2. Во втором так же. Далее на координатной плоскости отмечаем точки с координаты и, полученными ранее. Например точка K ( 2;1) и точка L (3;3). Обратите внимание, что в ответе координаты точки А мы пишем именно в таком порядке, т.к. На первом месте значение х, а на втором у. Когда вы отметили точки, вы вполне можете провести через них прямую, сделайте это. И лучше провести ее через всю плоскость, а не от точки до точки. Удачи!