Объяснение:
Найдем корни:
А теперь получили 2 неравенства. Если я правильно понимаю, что тут написано, а я не использую переводчик, знак неравенства строгой. Если не понимаю, то нестрогий:
Откуда находим m:
1)
2)
А теперь ищем пересечение!
Объяснение:
Найдем корни:
А теперь получили 2 неравенства. Если я правильно понимаю, что тут написано, а я не использую переводчик, знак неравенства строгой. Если не понимаю, то нестрогий:
Откуда находим m:
1)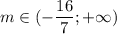
2)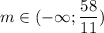
А теперь ищем пересечение!