Задача 1. В цилиндре проведена параллельно оси плоскость, отсекающая от окружности дугу в 120º. Длина оси равна 5, ее расстояние от секущей плоскости 2. Определите площадь сечения, объем и площадь полной поверхности цилиндра.
Задача 2.
Радиус основания конуса равен 20 см, образующая – 20,5 см. Конус пересечен плоскостью, параллельной основанию , на расстоянии 1,5 см от его вершины. Найдите радиус полученного сечения, объем и площадь полной поверхности конуса.
Задача 3. Прямоугольный параллелепипед со сторонами 6 дм и 8 дм и высотой, равной 14 дм, вписан в цилиндр. Найдите радиус основания цилиндра, площадь осевого сечения цилиндра, площадь полной поверхности цилиндра и параллелепипеда
ответ:1)15,2%;
2)81 т
3) 8;6;5
4) 20 дней
Объяснение: 1)15,2%
1 )процентное содержание меди в руде это отношение количества меди к количестве руды ×100%
Тогда 34,2/225×100%=15,2%
2)Если за 3 ч на мельнице смололи 27 т пшеничной муки, за 9 часов смололи в 3 раза больше(9:3=3) т.е 3×27=81 т
3) Если на 3 стакана вишни кладёт 2 стакана сахара,то на 1 стакан вишни кладут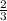
стакана сахара
На 12 стаканов вишни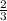
×12=8 стаканов сахара
На 10 стаканов вишни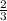
×10=6
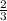стаканов сахара
На 7,5 стаканов вишни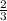
×7,5=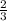
×
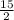= 5 стаканов сахара
4)Если 15 рабочих закончили отделку квартир в новом доме за 24 дня, то одно,
за 1 день 15 рабочих выполнят 1/24 часть работы
за 1 день 1 рабочий выполнить (1/24)/15=1/360 часть работы
за 1 день 18 рабочих выполнять 18/360 часть работы
Тогда на всю работу уйдет 360/18=20 дней
Для нахождения решения корней x2 - 6x = 16 полного квадратного уравнения мы начнем с того, что перенесем 16 в левую часть уравнения:
x2 - 6x - 16 = 0.
Для решения уравнения будем использовать формулы для поиска дискриминанта и корней уравнения через дискриминант.
D = b2 - 4ac = (-6)2 - 4 * 1 * (-16) = 36 + 64 = 100;
Корни уравнения мы вычислим по следующим формулам:
x1 = (-b + √D)/2a = (6 + √100)/2 * 1 = (6 + 10)/2 = 16/2 = 8;
x2 = (-b - √D)/2a = (6 - √100)/2 * 1 = (6 - 10)/2 = -4/2 = -2.
ответ: x = 8; x = -2.
Объяснение: