Допустим, цена изначально равнялась Р. С наступлением зимы цена увеличилась на х процентов, и стала равняться Р (1+х/100). Весной цена уменьшилась снова на х процентов, и стала равняться, соответственно, Р (1+х/100) (1-х/100). В тоже время, эта новая цена по условию на 4 % меньше изначальной, т. е равна Р (1-4/100)=Р (1-0.04). Приравниваем: Р (1+х/100)(1-х/100)=Р (1-0.04). Изначальная цена Р, как ей и положено, сокращается. Произведение суммы на разность равно разности квадратов. Получаем 1- (х/100)^2=1-0.04, т. е. (х/100)^2=0.04, т. е. х/100=0.2. Таким образом, цену повышали/ снижали на х=0.2*100=20%.
1. Упростить выражения нельзя, поэтому просто подставим
4
Теперь с другим знаком, на деле это будет вторая дробь, только у а противположный знак
во втором примере удобно представить икс и игрик в виде направильных дробей, тогда 1= -2=-
произведем вычисления 11*3/6=11/2
-11*2/4=11/2.
11/2-11/2=0
2. Выражение представленное в виде дроби имеет смысл тогда и только тогда, когда знаменатель не равен нулю, соответственно
А-3, т.к. если икс равен минус 2, то 2-2=0 а на 0 делить нельзя
Б-4, т.к. в знаменателе перменной нет
В -2, т.к. произведение двух выражений равно нулю, когда хотя бы 1 равен нулю, а значит чтобы произведение не было равно нулю, то ни одно из них не должно равнятся нулю, отсюда исключаем 2 и -2
наступлением зимы цена увеличилась на х
процентов, и стала равняться Р (1+х/100).
Весной цена уменьшилась снова на х процентов,
и стала равняться, соответственно, Р (1+х/100)
(1-х/100). В тоже время, эта новая цена по
условию на 4 % меньше изначальной, т. е равна
Р (1-4/100)=Р (1-0.04). Приравниваем: Р
(1+х/100)(1-х/100)=Р (1-0.04). Изначальная цена
Р, как ей и положено, сокращается.
Произведение суммы на разность равно
разности квадратов. Получаем 1-
(х/100)^2=1-0.04, т. е. (х/100)^2=0.04, т. е.
х/100=0.2. Таким образом, цену повышали/
снижали на х=0.2*100=20%.
Объяснение:
1. Упростить выражения нельзя, поэтому просто подставим
Теперь с другим знаком, на деле это будет вторая дробь, только у а противположный знак
во втором примере удобно представить икс и игрик в виде направильных дробей, тогда 1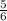 =
=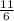 -2
-2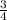 =-
=-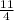
произведем вычисления 11*3/6=11/2
-11*2/4=11/2.
11/2-11/2=0
2. Выражение представленное в виде дроби имеет смысл тогда и только тогда, когда знаменатель не равен нулю, соответственно
А-3, т.к. если икс равен минус 2, то 2-2=0 а на 0 делить нельзя
Б-4, т.к. в знаменателе перменной нет
В -2, т.к. произведение двух выражений равно нулю, когда хотя бы 1 равен нулю, а значит чтобы произведение не было равно нулю, то ни одно из них не должно равнятся нулю, отсюда исключаем 2 и -2