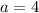Зная количество питательных веществ (n), необходимых взрослому человеку в сутки, можно вычислить среднее количество этих веществ (М) за любой промежуток времени (t), по формуле М=n*t. Сколько килограммов белков необходимо взрослому человеку в год (365 дн.), если в сутки он должен потреблять их 80г?
Алдымен өзіңді өзің таны» дейді атақты Сократ дана. Рим саясаткері және әйгілі шешені Цицеронның «Сократ тұңғыш рет филсофияны аспаннан жерге түсірді» деп баға беретіні де осы сөзі үшін екені даусыз. Иә, адам Тәңірдің ерекше жаратылысы. Адамзат өзінің кемел ақыл-парасатымен барлық әлемді меңгерсе де, өзінің адам ретіндегі сыры мен құпияларына тереңдей алған жоқ. Демек, адамтану ғылымы ешқашан аяқталмайды деген сөз. Десе де адам өзін-өзі тануға барынша әрекеттеніп, ол талпынысынан бір сәт бас тартқан емес. Өйткені, Абайша айтқанда, а әрқашан «білсем екен демекілікпен» өмір сүріп келеді. Әрі соның жолында «не көрсе соған талпынумен» тіршілік кешуде. Бұл да а тән хикмет.
Адам өзінің өткенінен сабақ алып, болашағын жоспарлай алуымен ғана адам болып тұрған жоқ па?! Тіршілік иелері ішінде адам ғана өзінің бастауын танып, болмысын білуге құштарлық таныта алады. Сол себепті адам өзінің қашан, қалай әрі неден жаралғанын білгісі келеді. Бірақ бұл жағынан әртүрлі жорамал айтылып, пікір алуандығы туатыны заңды. Сондықтан а ң жаратылысы туралы толғанып, соны зерттеуге өмірін сарп еткен ғұламалардың қатары көп. Бүгінде адамның жаратылуы туралы пікірлер мен көзқарастар баршылық. Барлық жорамалдар мен зерттеулерді саралай келе нақты үш түрлі болжамның аясына топтастыруға болады.
Нұрсерік ТІЛЕУҚАБЫЛ, тарих ғылымдарының магистрі
Объяснение:
Первый модуль обращается в ноль при x=-2, второй - при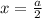
.
Пусть сначала
Тогда уравнение принимает вид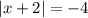
и, очевидно, не имеет решений.
Пусть теперь
Если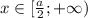
, то оба модуля раскрываются с плюсом и уравнение принимает вид:
Полученный x будет корнем уравнения, если он принадлежит рассматриваемому отрезку, то есть если
удовлетворяет системе неравенств
Решение системы: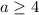
Если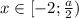
, то уравнение принимает вид
Полученный x будет корнем уравнения, если
удовлетворяет системе:
Решение системы: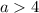
Пусть, наконец,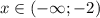
. Тогда уравнение принимает вид
Полученный x будет корнем уравнения, если
удовлетворяет системе:
Эта система не имеет решений.
Теперь пусть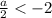
, то есть 
.
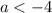Если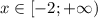
, то
Система:
Нет решений.
Если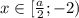
, то
Система:
Решение системы: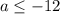
И наконец, если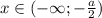
, то
Система:
Решение: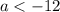
Из вышесказанного очевидно, что
При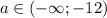
- два решения
При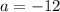
- одно решение
При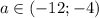
- нет решений
При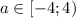
- нет решений
При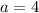
- одно решение
При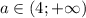
- два решения
Таким образом, уравнение имеет одно решение пр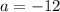и
и 