Коли об'єм що займає газ зменшили на 40% а температуру знизили на 84к тиск газу зріс на 20%.Яка початкова температура газу?

Показать ответ

Ответ:

matveq888

07.11.2022 15:15

Дано:

U₁ = 190 В

I₁ = 1,9 А

U₂ = 170 В

I₂ = 2 А

Найти R.

Пусть сопротивление вольтметра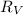 R_V ,

а сопротивление амперметра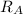 R_A .

Рассмотрим первую схему: резистор и амперметр соединены последовательно, а вольтметр включен к ним параллельно.

$I_1 = \frac{U_1}{R + R_A}$

$R + R_A = \frac{U_1}{I_1}$

$U_{CD} = U_1$

Рассмотрим вторую схему:

$I_R = \frac{U_2}{R}$

$I_V = \frac{U_2}{R_V}$

I_2 = I_R + I_V

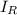где I_R это ток, текущий через резистор.

I_V это ток, текущий через вольтметр.

$I_2 = \frac{U_2}{R} + \frac{U_2}{R_V}$

$U_{CD} = U_2 + U_{A2}$

$U_{A2} = I_2\cdot R_A$

$U_{CD} = U_2 + I_2\cdot R_A$

Так как подаваемое напряжение на клеммы C и D на первой и второй схемах одинаковое, то

$U_1 = U_2 + I_2\cdot R_A$

Отсюда найдем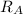 R_A

$U_1 - U_2 = I_2\cdot R_A$

$R_A = \frac{U_1 - U_2}{I_2}$

И подставим это в самое первое уравнение

$R + R_A = \frac{U_1}{I_1}$

$R + \frac{U_1 - U_2}{I_2} = \frac{U_1}{I_1}$

$R = \frac{U_1}{I_1} - \frac{U_1 - U_2}{I_2}$

R = (190В/1,9А) - (190В - 170В)/2А = 100 Ом - (20В/2А) = 100 Ом - 10 Ом =

= 90 Ом.

ответ. 90 Ом.

0,0(0 оценок)

Ответ:

seminalydmila

06.06.2021 15:34

Уравнение движения первого тела x1=-v0t+0.5at^2; a=g*sin(b), b- угол наклона плоскости.
для второго тела x2=v0t+0.5at^2;
Скорость первого тела равна: v1=x1'=-v0+at1; В момент остановки она равна нулю: v0=at1; Отсюда t1=v0/a;
Находим расстояния, пройденные телами за это время t1;
x1=-v0*v0/a+0.5a*v0^2/a^2;
x1=-v0^2/a+0.5v0^2/a;
x1=-0.5v0^2/a; (нас интересует отношение расстояний, поэтому берём модуль числа) x1=0.5v0^2/a;

x2=v0*v0/a+0.5a*v0^2/a^2;
x2=1.5v0^2/a;

x2/x1=(1.5v0^2/a)/(0.5v0^2/a);
x2/x1=3. Второе тело путь в три раза больше, чем первое.

0,0(0 оценок)

Популярные вопросы: Физика