1. Дана трапеция WXYZ. WX=YZ, докажите, что ее можно вписать в окружность. 2. В трапецию KLMN вписана окружность. MN, KL - боковые стороны. MN=6 см, KL в 2,5 раза больше MN. Найдите среднюю линию трапеции KLMN.

3. Дан треугольник RST, такой что RT является диаметром окружности описанной около него. Угол STR=96 градусов. Найдите угол TRS.

4. Четырехугольник вписан в окружность, его диагонали с одной из сторон образуют равные 30 градусам углы. Какой фигурой может быть этот четырехугольник, обоснуйте свой ответ (докажите).

1.

Катеты фиолетового треугольника: 16; 6

Гипотенуза равна: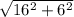

Гипотенуза фиолетового треугольника равна: 17.1.

2.

Чтобы найти наибольший катет бледно-красного, вычтим те 4 сантиметра с нашей гипотенузы: 17.1-4 = 13.1

Теперь к этому числу добавим те 9 сантиметров (в правой нижней стороне красного треугольника): 13.1+9 = 22.1

Теперь нам известно 2 катета бледно-красного треугольника: 22.1; 7.

Гипотенуза её равна:

Вычтим с этого числа те 2 сантиметров(в правом верхнем углу бледно-красного треугольника): 23.18-2 = 21.18.

3.

Теперь нам известна гипотенуза жёлтого треугольника, и его катет.

Второй катет равен: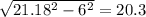

Теперь мы знаем 2 катета, и гипотенузу желтого треугольника.

4.

Прибавим к наибольшому катету 5 и 1(в правом и левом нижнем углу синего треугольника): 20.3+6 = 26.3.

Теперь нам известно 2 катета синего треугольника: 12; 26.3.

Гипотенуза равна: .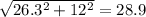

5.

Вычтим 11 сантиметров с гипотенузы синего треугольника (левый нижний угол зелёного треугольника): 28.9-11 = 17.9.

Теперь нам известно 2 катета зелёного треугольника: 14; 17.9.

Гипотенуза равна: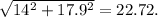

6.

Нам известна гипотенуза, и один катет розового треугольника: 16; 22.72.

Второй катет равен: .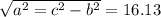

7. Прибавим к этому числу 5 сантиметров (нижний левый угол голубого треугольника): 16.13+5 = 21.13.

Теперь нам известно 2 катета: 5; 21.13

Найдём гипотенузу: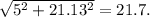  

Вывод: самая верхняя гипотенуза равна 21,71 сантиметров.

72 см²

Объяснение:

1. Прямоугольный Δ АСК. ∠ К = 60° ⇒ ∠А = 180 - 90 - 60 = 30° ⇒ СК = 1/2АК = 4√3, как катет, лежащий напротив угла в 30°.

2. Прямоугольный Δ СРК. ∠К = 60° ⇒ ∠ С = 180 - 90 - 60 = 30°

⇒ РК = 1/2 СК = 2√3, как катет, лежащий напротив угла в 30°.

По теореме Пифагора СР = √(СК² - РК²) = √36 = 6

3. Δ АВМ =  Δ СРК по гипотенузе и острому углу ⇒ АМ = РК = 2√3 ⇒ МЗ = 8√3 - 2√3 - 2√3 = 4√3.

4. В 4-х угольнике ВСРМ противоположные стороны попарно параллельны, углы = 90° ⇒ является прямоугольником. ⇒ ВС = МР = 4√3

5. S трапеции АВСК = СР * (ВС + АК)/2 = 6 * (4√3 + 8√3) = 72√3 см²